题目内容
已知实数x、y满足
,则u=
的取值范围是
|
| x+y |
| x |
[2,4]
[2,4]
.分析:①画可行域②明确目标函数几何意义,目标函数表示动点P(x,y)与定点O(0,0)连线斜率k再加1,③过O做直线与可行域相交可计算出直线PO斜率,从而得出所求目标函数范围.
解答: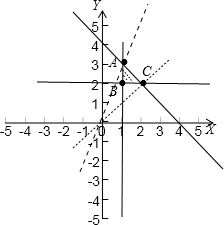 解:先画出可行域如图:
解:先画出可行域如图:
因为目标函数表示动点P(x,y)与定点O(0,0)连线斜率k再加1;
由图可知;
KOC最小,KOA最大;
联立
可得
,A(1,3)
联立
可得
,C(2,2).
故:KOC=
=1,KOA=
=3,
∴1≤KOP≤3,
所以:u=
=1+
∈[2,4].
故答案为:[2,4].
 解:先画出可行域如图:
解:先画出可行域如图:因为目标函数表示动点P(x,y)与定点O(0,0)连线斜率k再加1;
由图可知;
KOC最小,KOA最大;
联立
|
|
联立
|
|
故:KOC=
| 2-0 |
| 2-0 |
| 3-0 |
| 1-0 |
∴1≤KOP≤3,
所以:u=
| x+y |
| x |
| y-0 |
| x-0 |
故答案为:[2,4].
点评:本题考查线性规划问题,难点在于目标函数几何意义,近年来高考线性规划问题高考数学考试的热点,数形结合是数学思想的重要手段之一,是连接代数和几何的重要方法.随着要求数学知识从书本到实际生活的呼声不断升高,线性规划这一类新型数学应用问题要引起重视.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
已知实数x,y满足
-
=1(a>0,b>0),则下列不等式中恒成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|<
| ||
B、y>-
| ||
C、|y|>-
| ||
D、y<
|