题目内容
若α、β∈(
,π),且tanα<cotβ,那么必有( )
| π |
| 2 |
A.α+β>
| B.α+β<
| C.α>β | D.α<β |
∵α、β∈(
,π),
∴-π<-β<-
,
<
-β<π,
又cotβ=tan(
-β)=tan(
-β),tanα<cotβ,
∴tanα<tan(
-β),α、
-β∈(
,π),又y=tanx在(
,π)上单调递增,
∴α<
-β,即α+β<
.
故选B.
| π |
| 2 |
∴-π<-β<-
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
又cotβ=tan(
| π |
| 2 |
| 3π |
| 2 |
∴tanα<tan(
| 3π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴α<
| 3π |
| 2 |
| 3π |
| 2 |
故选B.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 在一个周期内,当
在一个周期内,当 时,
时, 取得最小值
取得最小值 ;当
;当 时,
时, 时,
时, 的值为 ( )
的值为 ( ) 取值有关
取值有关 的部分图象如图所示,则函数表达式为( ).
的部分图象如图所示,则函数表达式为( ).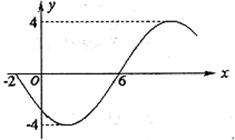
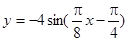






 .
. 、
、 的值;
的值; 的值.
的值.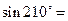 ( )
( )


