题目内容
P(x,y)是曲线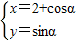 (α为参数)上任意一点,则(x-5)2+(y+4)2的最大值为 .
(α为参数)上任意一点,则(x-5)2+(y+4)2的最大值为 .
【答案】分析:将曲线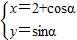 消去参数α,得以(2,0)为圆心,半径为1的圆.结合坐标系内两点间的距离公式,得到(x-5)2+(y+4)2表示动点P与Q(5,-4)之间距离的平方,由此根据圆的性质即可得到(x-5)2+(y+4)2的最大值.
消去参数α,得以(2,0)为圆心,半径为1的圆.结合坐标系内两点间的距离公式,得到(x-5)2+(y+4)2表示动点P与Q(5,-4)之间距离的平方,由此根据圆的性质即可得到(x-5)2+(y+4)2的最大值.
解答:解:∵曲线 (α为参数),消去参数得(x-2)2+y2=1
(α为参数),消去参数得(x-2)2+y2=1
∴点P在以(2,0)为圆心,半径为1的圆上运动
设Q(5,-4),可得|PQ|=
∴(x-5)2+(y+4)2表示动点P与Q(5,-4)之间距离的平方,
∵|PQ|最大值=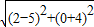 +1=5+1=6
+1=5+1=6
∴|PQ|2最大值=36,即得(x-5)2+(y+4)2的最大值为36
故答案为:36
点评:本题给出圆上的动点P,求点P到Q(5,-4)之间距离的最大值,着重考查了曲线方程的化简、圆的性质和两点间的距离公式等知识,属于基础题.
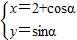 消去参数α,得以(2,0)为圆心,半径为1的圆.结合坐标系内两点间的距离公式,得到(x-5)2+(y+4)2表示动点P与Q(5,-4)之间距离的平方,由此根据圆的性质即可得到(x-5)2+(y+4)2的最大值.
消去参数α,得以(2,0)为圆心,半径为1的圆.结合坐标系内两点间的距离公式,得到(x-5)2+(y+4)2表示动点P与Q(5,-4)之间距离的平方,由此根据圆的性质即可得到(x-5)2+(y+4)2的最大值.解答:解:∵曲线
 (α为参数),消去参数得(x-2)2+y2=1
(α为参数),消去参数得(x-2)2+y2=1∴点P在以(2,0)为圆心,半径为1的圆上运动
设Q(5,-4),可得|PQ|=

∴(x-5)2+(y+4)2表示动点P与Q(5,-4)之间距离的平方,
∵|PQ|最大值=
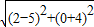 +1=5+1=6
+1=5+1=6∴|PQ|2最大值=36,即得(x-5)2+(y+4)2的最大值为36
故答案为:36
点评:本题给出圆上的动点P,求点P到Q(5,-4)之间距离的最大值,着重考查了曲线方程的化简、圆的性质和两点间的距离公式等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设点P(x,y)是曲线
+
=1上的点,又点F1(-4,0),F2(4,0),下列结论正确的是( )
|
|
| A、|PF1|+|PF2|=10 |
| B、|PF1|+|PF2|<10 |
| C、|PF1|+|PF2|≤10 |
| D、|PF1|+|PF2|>10 |