题目内容
已知点F1（-4，0），F2（4，0），又P（x，y）是曲线
+
=1上的点，则（ ）
| |x| |
| 5 |
| |y| |
| 3 |
分析：根据题意，曲线
+
=1表示的图形是图形是如图所示的菱形ABCD，而满足|PF1|+|PF2|=10的点的轨迹恰好是以A、B、C、D为顶点的椭圆，由此结合椭圆的定义即可得到|PF1|+|PF2|≤10．
| |x| |
| 5 |
| |y| |
| 3 |
解答：解：∵F1（-4，0），F2（4，0），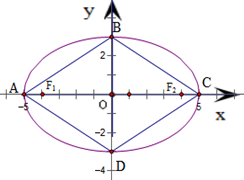
∴满足|PF1|+|PF2|=10的点在以F1、F2为焦点，
2a=10的椭圆上
可得椭圆的方程为
+
=1，
∵曲线
+
=1表示的图形是图形是以A（-5，0），
B（0，3），C（5，0），D（0，-3）为顶点的菱形
∴由图形可得菱形ABCD的所有点都不在椭圆的外部，
因此，曲线
+
=1上的点P，必定满足|PF1|+|PF2|≤10
故选：C
∴满足|PF1|+|PF2|=10的点在以F1、F2为焦点，
2a=10的椭圆上
可得椭圆的方程为
| x2 |
| 25 |
| y2 |
| 9 |
∵曲线
| |x| |
| 5 |
| |y| |
| 3 |
B（0，3），C（5，0），D（0，-3）为顶点的菱形
∴由图形可得菱形ABCD的所有点都不在椭圆的外部，
因此，曲线
| |x| |
| 5 |
| |y| |
| 3 |
故选：C
点评：本题给出曲线方程，求曲线上的点P满足的条件．着重考查了椭圆的定义与标准方程、简单几何性质等知识，属于中档题．
练习册系列答案
相关题目
-
=1
-
=1（y＞0）
-
=1或 
-
=1
-
=1
-
=1（x＞0）
上的点，则（ ）