题目内容
(2011•福建模拟)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程为ρ2=
;
(Ⅰ)若以极点为原点,极轴所在的直线为x轴,求曲线C的直角坐标方程.
(Ⅱ)若P(x,y)是曲线C上的一个动点,求3x+4y的最大值.
已知曲线C的极坐标方程为ρ2=
| 36 | 4cos2θ+9sin2θ |
(Ⅰ)若以极点为原点,极轴所在的直线为x轴,求曲线C的直角坐标方程.
(Ⅱ)若P(x,y)是曲线C上的一个动点,求3x+4y的最大值.
分析:(Ⅰ)先将曲线C的极坐标方程化为4(ρcosθ)2+9(ρsinθ)2=36,利用x=ρcosθ,y=ρsinθ,即可得到曲线C的直角坐标方程;
(Ⅱ)利用参数法设点的坐标,设P(3cosθ,2sinθ),则3x+4y=9cosθ+8sinθ=
sin(θ+φ),根据sin(θ+φ)的最大值,可确定3x+4y的最大值.
(Ⅱ)利用参数法设点的坐标,设P(3cosθ,2sinθ),则3x+4y=9cosθ+8sinθ=
| 145 |
解答:解:(Ⅰ)∵曲线C的极坐标方程为ρ2=
;
∴4(ρcosθ)2+9(ρsinθ)2=36
∵x=ρcosθ,y=ρsinθ
∴4x2+9y2=36
∴
+
=1;(3分)
(Ⅱ)设P(3cosθ,2sinθ),
则3x+4y=9cosθ+8sinθ=
sin(θ+φ)(6分)
∵θ∈R,
∴当sin(θ+φ)=1时,3x+4y的最大值为
(7分)
| 36 |
| 4cos2θ+9sin2θ |
∴4(ρcosθ)2+9(ρsinθ)2=36
∵x=ρcosθ,y=ρsinθ
∴4x2+9y2=36
∴
| x2 |
| 9 |
| y2 |
| 4 |
(Ⅱ)设P(3cosθ,2sinθ),
则3x+4y=9cosθ+8sinθ=
| 145 |
∵θ∈R,
∴当sin(θ+φ)=1时,3x+4y的最大值为
| 145 |
点评:本题以曲线的极坐标方程为载体,考查极坐标与直角坐标方程的互化,考查参数法,解题的关键是利用x=ρcosθ,y=ρsinθ
.
.

练习册系列答案
相关题目
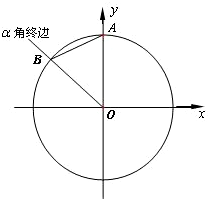 (2011•福建模拟)如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交与点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.
(2011•福建模拟)如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交与点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.