Question

【题目】在如图所示的几何体中，底面ABCD中，AB⊥AD，AD＝2，AB＝3，BC＝BE＝7，△DCE是边长为6的正三角形．

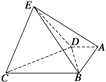
(1)求证：平面DEC⊥平面BDE；

(2)求点A到平面BDE的距离．

Answer 1

【答案】（1）见解析；（2）．

【解析】试题分析：（1）由勾股定理及逆定理可得，从而有线面垂直，于是可得面面垂直；

（2）到平面的距离可用体积法求得， ．

试题解析：

(1)证明　因为AB⊥AD，AD＝2，AB＝3，所以BD＝，

又因为BC＝7，CD＝6，所以根据勾股定理可得BD⊥CD，

因为BE＝7，DE＝6，同理可得BD⊥DE．

因为DE∩CD＝D，DE平面DEC，CD平面DEC，

所以BD⊥平面DEC．因为BD平面BDE，

所以平面DEC⊥平面BDE．

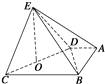
(2)解　如图，取CD的中点O，连接OE，

因为△DCE是边长为6的正三角形，

所以EO⊥CD，EO＝3，

易知EO⊥平面ABCD，

则VE－ABD＝××2×3×3＝3，

又因为直角三角形BDE的面积为×6×＝3，

设点A到平面BDE的距离为h，则由VE－ABD＝VA－BDE，

得×3h＝3，所以h＝，所以点A到平面BDE的距离为．