题目内容
【题目】某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图所示，据此解答如下问题：
(1)求高三(1)班全体女生的人数；
(2)求分数在[80,90)之间的女生人数，并计算频率分布直方图中[80,90)之间的矩形的高；
(3)若要从分数在[80,100]之间的试卷中任取两份分析女生失分情况，在抽取的试卷中，求至少有一份分数在[90,100]之间的概率．
【答案】（1）25
（2）0.016
（3）0.6
【解析】试题分析：（1）解：设全班女生人数为
， 
（2） 根据题意，由于分数在
之间的女生人数25-21=4人，根据比例关系得0.016
（3）设六个人编号为1,2,3,4,5,6.所有可能根据列举法得（1,2）（1,3）（1,4）（1,5）（1,6）（2,2）（2,3）（2,4）（2,5）（2,6）（3,4）（3,5）（3,6）（4, 5）（4,6）（5,6）15个基本事件，其中符合的是（1,5）（1,6）（2,5）（2,6）（3,5）（3,6）（4,5）（4,6）（5,6）9个基本事件，
所以所求概率为
【题目】学校为了了解高三学生每天自主学习中国古典文学的时间，随机抽取了高三男生和女生各50名进行问卷调查，其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”，否则为“非古文迷”，调查结果如表：
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
（1）根据表中数据判断能否有
的把握认为“古文迷”与性别有关？
（2）先从调查的女生中按分层抽样的方法抽出5人进行理科学习时间的调查，求所抽取的5人中“古文迷”和“非古文迷”的人数；
（3）现从（2）中所抽取的5人中再随机抽取3人进行体育锻炼时间的调查，记这3人中“古文迷”的人数为
，求随机变量
的分布列与数学期望．
参考数据：
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
参考公式：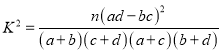 
，其中
．
