题目内容
【题目】已知函数f(x)=4sinxcos2( ![]() +
+ ![]() )﹣cos2x.
)﹣cos2x.
(1)将函数y=f(2x)的图象向右平移 ![]() 个单位长度得到函数y=g(x)的图象,求函数g(x)在x∈[
个单位长度得到函数y=g(x)的图象,求函数g(x)在x∈[ ![]() ,
, ![]() ]上的值域;
]上的值域;
(2)已知a,b,c分别为△ABC中角A,B,C的对边,且满足b=2,f(A)= ![]() a=2bsinA,B∈(0,
a=2bsinA,B∈(0, ![]() ),求△ABC的面积.
),求△ABC的面积.
【答案】
(1)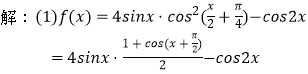
=2sinx﹣2sin2x﹣cos2x=2sinx﹣1,
∴函数f(2x)=2sin2x﹣1 的图象向右平移 ![]() 个单位得到函数
个单位得到函数
g(x)=2sin2(x﹣ ![]() )﹣1=2sin(2x﹣
)﹣1=2sin(2x﹣ ![]() )﹣1的图象
)﹣1的图象
∵x∈[ ![]() ,
, ![]() ],∴2x﹣
],∴2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
当x= ![]() 时,g(x)min=﹣2;当x=
时,g(x)min=﹣2;当x= ![]() 时,g(x)max=1,所求值域为[﹣2,1]
时,g(x)max=1,所求值域为[﹣2,1]
(2)由已知 ![]() a=2bsinA及正弦定理得:
a=2bsinA及正弦定理得: ![]() sinA=2sinBsinA
sinA=2sinBsinA
∴sinB= ![]() ,∵0
,∵0 ![]() ,∴B=
,∴B= ![]()
由f(A)= ![]() ﹣1,得sinA=
﹣1,得sinA= ![]() .
.
又a= ![]() b<b,∴A=
b<b,∴A= ![]() ,
,
由正弦定理得:a= ![]() ,
,
∴S△ABC= ![]() absinC=
absinC= ![]() ×2×
×2× ![]() =
= ![]()
【解析】(1)利用三角函数恒等变换的应用化简可得f(x)=2sinx﹣1,由题意可求g(x)=2sin(2x﹣ ![]() )﹣1,由x∈[
)﹣1,由x∈[ ![]() ,
, ![]() ],可求2x﹣
],可求2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],利用正弦函数的性质可求值域.(2)由已知及正弦定理得:
],利用正弦函数的性质可求值域.(2)由已知及正弦定理得: ![]() sinA=2sinBsinA,可求sinB=
sinA=2sinBsinA,可求sinB= ![]() ,结合范围0
,结合范围0 ![]() 可求B=
可求B= ![]() ,进而可求sinA,由正弦定理得a,利用三角形面积公式即可计算得解.
,进而可求sinA,由正弦定理得a,利用三角形面积公式即可计算得解.
【考点精析】认真审题,首先需要了解正弦函数的单调性(正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数),还要掌握正弦定理的定义(正弦定理:
上是减函数),还要掌握正弦定理的定义(正弦定理:![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.

【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50 名,其中每天玩微信超过6 小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“微信控”与”性别“有关?
(2)现从调查的女性用户中按分层抽样的方法选出5 人并从选出的5 人中再随机抽取3 人赠送200 元的护肤品套装,记这3 人中“微信控”的人数为X,试求X 的分布列与数学期望. 参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |