题目内容
设数列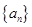 的前
的前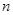 项和为
项和为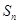 ,且对任意
,且对任意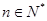 都有:
都有: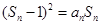 ;
;
(1)求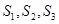 ;
;
(2)猜想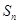 的表达式并证明.
的表达式并证明.
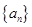 的前
的前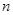 项和为
项和为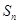 ,且对任意
,且对任意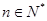 都有:
都有: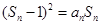 ;
;(1)求
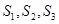 ;
;(2)猜想
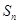 的表达式并证明.
的表达式并证明.(1)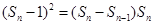
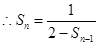 , 又
, 又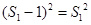 ,
,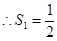
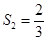 ,
,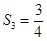 , (2)猜想
, (2)猜想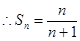 下面用数学归纳法证明(略)
下面用数学归纳法证明(略)
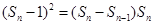
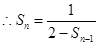 , 又
, 又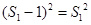 ,
,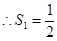
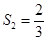 ,
,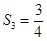 , (2)猜想
, (2)猜想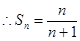 下面用数学归纳法证明(略)
下面用数学归纳法证明(略)试题分析:(1)
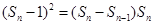
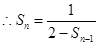 , 又
, 又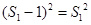 ,
,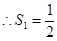
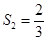 ,
,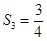 ,
, (2)猜想
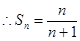 下面用数学归纳法证明:
下面用数学归纳法证明:1°当n=1时,
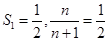 ,猜想正确;
,猜想正确;2°假设当n=k时,猜想正确,即
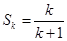 ,
,那么,n=k+1时,由
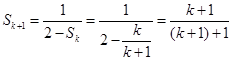 ,猜想也成了,
,猜想也成了,综上知,
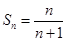 对一切自然数n均成立。
对一切自然数n均成立。点评:中档题,涉及数列中
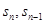 的关系,确定数列的特征,往往要建立两式,相减或相除等。利用数学归纳法证明问题,要注意其步骤规范,做好“两步一结”。
的关系,确定数列的特征,往往要建立两式,相减或相除等。利用数学归纳法证明问题,要注意其步骤规范,做好“两步一结”。
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
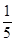 n5+
n5+ n4+
n4+ n3-
n3- n.
n.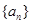 满足
满足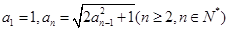
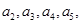 并猜想
并猜想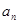 的表达式
的表达式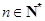 且
且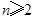 ,证明:
,证明: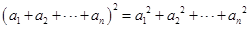
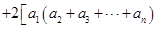
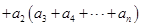
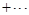
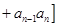 .
.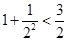 ,
,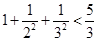 ,
,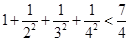 ,……则可归纳出式子(
,……则可归纳出式子(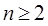 )( )
)( )


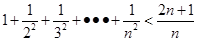
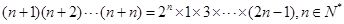 ”时,从“
”时,从“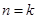 ”变到 “
”变到 “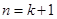 ”时,左边应增乘的因式是
”时,左边应增乘的因式是 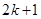
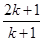

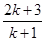
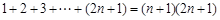 时,当
时,当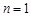 时左边表达式是 ;从
时左边表达式是 ;从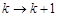 需增添的项的是 .
需增添的项的是 .