题目内容
已知多项式f(n)=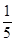 n5+
n5+ n4+
n4+ n3-
n3- n.
n.
(1)求f(-1)及f(2)的值;
(2)试探求对一切整数n,f(n)是否一定是整数?并证明你的结论.
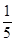 n5+
n5+ n4+
n4+ n3-
n3- n.
n.(1)求f(-1)及f(2)的值;
(2)试探求对一切整数n,f(n)是否一定是整数?并证明你的结论.
(1)0,17(2)见解析
(1)f(-1)=0,f(2)=17
(2)先用数学归纳法证明,对一切正整数n,f(n)是整数.
①当n=1时,f(1)=1,结论成立.
②假设当n=k(k≥1,k∈N)时,结论成立,即f(k)=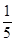 k5+
k5+ k4+
k4+ k3-
k3- k是整数,则当n=k+1时,f(k+1)=
k是整数,则当n=k+1时,f(k+1)=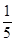 (k+1)5+
(k+1)5+ (k+1)4+
(k+1)4+ (k+1)3-
(k+1)3- (k+1)
(k+1)
=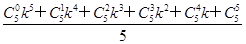 +
+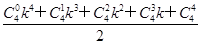
+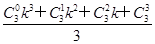 -
- (k+1)=f(k)+k4+4k3+6k2+4k+1.
(k+1)=f(k)+k4+4k3+6k2+4k+1.
根据假设f(k)是整数,而k4+4k3+6k2+4k+1显然是整数.
∴f(k+1)是整数,从而当n=k+1时,结论也成立.
由①、②可知对一切正整数n,f(n)是整数.
(Ⅰ)当n=0时,f(0)=0是整数
(Ⅱ)当n为负整数时,令n=-m,则m是正整数,由(Ⅰ)知f(m)是整数,
所以f(n)=f(-m)=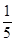 (-m)5+
(-m)5+ (-m)4+
(-m)4+ (-m)3-
(-m)3- (-m)
(-m)
=-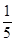 m5+
m5+ m4-
m4- m3+
m3+ m=-f(m)+m4是整数.
m=-f(m)+m4是整数.
综上,对一切整数n,f(n)一定是整数.
(2)先用数学归纳法证明,对一切正整数n,f(n)是整数.
①当n=1时,f(1)=1,结论成立.
②假设当n=k(k≥1,k∈N)时,结论成立,即f(k)=
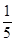 k5+
k5+ k4+
k4+ k3-
k3- k是整数,则当n=k+1时,f(k+1)=
k是整数,则当n=k+1时,f(k+1)=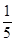 (k+1)5+
(k+1)5+ (k+1)4+
(k+1)4+ (k+1)3-
(k+1)3- (k+1)
(k+1)=
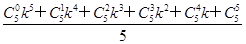 +
+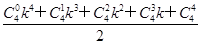
+
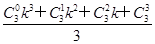 -
- (k+1)=f(k)+k4+4k3+6k2+4k+1.
(k+1)=f(k)+k4+4k3+6k2+4k+1.根据假设f(k)是整数,而k4+4k3+6k2+4k+1显然是整数.
∴f(k+1)是整数,从而当n=k+1时,结论也成立.
由①、②可知对一切正整数n,f(n)是整数.
(Ⅰ)当n=0时,f(0)=0是整数
(Ⅱ)当n为负整数时,令n=-m,则m是正整数,由(Ⅰ)知f(m)是整数,
所以f(n)=f(-m)=
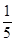 (-m)5+
(-m)5+ (-m)4+
(-m)4+ (-m)3-
(-m)3- (-m)
(-m)=-
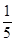 m5+
m5+ m4-
m4- m3+
m3+ m=-f(m)+m4是整数.
m=-f(m)+m4是整数.综上,对一切整数n,f(n)一定是整数.

练习册系列答案
相关题目

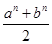 ≥
≥ n(a,b是非负实数,n∈N+)时,假设n
n(a,b是非负实数,n∈N+)时,假设n +
+ +…+
+…+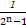 <n(n∈N*,n>1)时,第一步应验证的不等式是 .
<n(n∈N*,n>1)时,第一步应验证的不等式是 .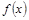 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且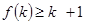 成立时,总可推出
成立时,总可推出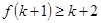 成立”,那么,下列命题总成立的是 ( )
成立”,那么,下列命题总成立的是 ( )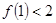 成立,则
成立,则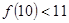 成立
成立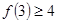 成立,则当
成立,则当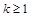 时,均有
时,均有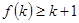 成立
成立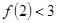 成立,则
成立,则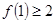 成立
成立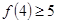 成立,则当
成立,则当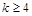 时,均有
时,均有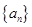 的前
的前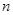 项和为
项和为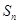 ,且对任意
,且对任意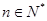 都有:
都有: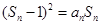 ;
;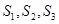 ;
;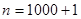 时它也成立,下列判断中,正确的是( )
时它也成立,下列判断中,正确的是( )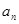 }的前n项和为
}的前n项和为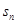 ,
,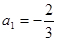 ,满足
,满足 ,计算
,计算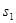 ,
,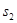 ,
,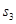 ,
,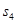 ,并猜想
,并猜想