题目内容

已知曲线C的极坐标方程是ρ=1，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=1+
t
2
y=2+
3
2
t
(t为参数）．
（1）写出直线l与曲线C的直角坐标方程；
（2）设曲线C经过伸缩变换
x′=2x
y′=y
得到曲线C′，设曲线C′上任一点为M（x，y），求x+2
3
y的最小值．
分析：（1）利用ρ2=x2+y2，将ρ=1转化成直角坐标方程，然后将直线的参数方程的上式化简成t=2（x-1）代入下式消去参数t即可；
（2）根据伸缩变换公式求出变换后的曲线方程，然后利用参数方程表示出曲线上任意一点，代入x+2
3
y，根据三角函数的辅助角公式求出最小值．
解答：解：（1）直线l的参数方程为
x=1+
t
2
y=2+
3
2
t
(t为参数）．
由上式化简成t=2（x-1）代入下式得l：
3
x-y+2-
3
=0
根据ρ2=x2+y2，进行化简得C：x2+y2=1（2分）
（2）∵
x′=2x
y′=y
∴
x=
x′
2
y=y′
代入C得∴C′：
x2
4
+y2=1（5分）
设椭圆的参数方程
x=2cosθ
y=sinθ
(θ为参数）（7分）
则x+2
3
y=2cosθ+2
3
sinθ=4sin(θ+
π
6
)（9分）
则x+2
3
y的最小值为-4．（10分）
点评：本题主要考查了圆的极坐标方程与直线的参数方程转化成直角坐标方程，以及利用椭圆的参数方程求最值问题，属于基础题．
练习册系列答案
相关题目
2、已知曲线C的极坐标方程是ρ=4cosθ，那么它的直角坐标方程是
（x-2）2+y2=4
．
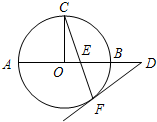精英家教网A（选修4-1：几何证明选讲）
如图，AB是⊙O的直径，C，F是⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D，连接CF交AB于点E．
求证：DE2=DB•DA．
B（选修4-2：矩阵与变换）
求矩阵
21
12
的特征值及对应的特征向量．
C（选修4-4：坐标系与参数方程）
已知曲线C的极坐标方程是ρ=2sinθ，直线l的参数方程是
x=-
3
5
t+2
y=
4
5
t
（t为参数）．
（Ⅰ）将曲线C的极坐标方程化为直角坐标方程；
（Ⅱ）设直线l与x轴的交点是M，N是曲线C上一动点，求MN的最大值．
D（选修4-5：不等式选讲）
已知m＞0，a，b∈R，求证：(
a+mb
1+m
)2≤
a2+mb2
1+m
．
精英家教网（坐标系与参数方程选做题）．
已知曲线C的极坐标方程是ρ=1，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是 
x=-1+4t
y=3t
（t为参数），则直线l与曲线C相交所成的弦的弦长为
 
．
（2013•文昌模拟）选修4-4：坐标系与参数方程
已知曲线C的极坐标方程是ρ=1，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程
x=1+
t
2
y=2+
3
2
t
(t为参数)．
（1）写出直线l的普通方程与曲线C的直角坐标方程；
（2）设曲线C经过伸缩变换
x′=3x
y′=y
得到曲线C′，设曲线C′上任一点为M（x，y），求x+2
3
y的最小值．
（坐标系与参数方程选做题）
已知曲线C的极坐标方程是ρ=6sinθ，以极点为坐标原点，极轴为x的正半轴，建立平面直角坐标系，直线l的参数方程是
x=
2
t-1
y=
2
2
t
(t为参数），则直线l与曲线C相交所得的弦的弦长为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网