Question

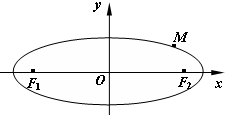（2013•盐城一模）如图，在平面直角坐标系xOy中，已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）经过点M（3

2

，

2

），椭圆的离心率e=

2 2

3

，F₁、F₂分别是椭圆的左、右焦点．
（1）求椭圆C的方程；
（2）过点M作两直线与椭圆C分别交于相异两点A、B．
①若直线MA过坐标原点O，试求△MAF₂外接圆的方程；
②若∠AMB的平分线与y轴平行，试探究直线AB的斜率是否为定值？若是，请给予证明；若不是，请说明理由．

Answer 1

分析：（1）利用椭圆的离心率化简方程，根据椭圆过点M（3

2

，

2

），即可求椭圆C的方程；
（2）①求得MA的中垂线方程、MF₂的中垂线方程，从而可得圆心与半径，即可求△MAF₂外接圆的方程；
②直线与椭圆方程联立，利用韦达定理，结合斜率公式，即可得到结论．

解答：解：（1）由椭圆的离心率e=

2 2

3

，可得a²=9b²，故椭圆方程为

x2

9b2

+

y2

b2

=1…（3分）
又椭圆过点M（3

2

，

2

），则

18

9b2

+

2

b2

=1，解得b²=4，
所以椭圆的方程为

x2

36

+

y2

4

=1…（5分）
（2）①记△MAF₂的外接圆的圆心为T．
因为kOM=

1

3

，所以MA的中垂线方程为y=-3x+5

2

，
又由M（3

2

，

2

），F₂（4

2

，0），得MF₂的中点为(

7 2

2

，

2

2

)，
而kMF2=-1，
所以MF₂的中垂线方程为y=-3x，
由

y=-3x y=x-3 2

，得T（

3 2

4

，-

9 2

4

） …（8分）
所以圆T的半径为

(4 2 - 3 2 4 )2+(0+ 9 2 4 )2

=

5 5

2

，
故△MAF₂的外接圆的方程为(x-

3 2

4

)2+(y+

9 2

4

)2=

125

4

…（10分）
②设直线MA的斜率为k，A（x₁，y₁），B（x₂，y₂）．（x₂＞x₁）
由题直线MA与MB的斜率互为相反数，
∴直线MB的斜率为-k．
联立直线MA与椭圆方程，可得（9k²+1）x²+18

2

k(1-3k)x+162k²-108k-18=0
∴x₁+x₂=-

18 2 k(1-3k)

9k2+1

，x2-x1=

36 2 k

9k2+1

…（13分）
又y2-y1=-k(x1+x2)+6

2

k=

12 2 k

9k2+1

∴kAB=

y2-y1

x2-x1

=

12 2 k 9k2+1

36 2 k 9k2+1

=

1

3

为定值…（16分）

点评：本题考查椭圆的标准方程，考查三角形的外接圆，考查直线与椭圆的位置关系，考查学生的计算能力，属于中档题．