题目内容
（2013•盐城一模）如图，在等腰三角形ABC中，底边BC=2，| AD |
| DC |
| AE |
| 1 |
| 2 |
| EB |
| BD |
| AC |
| 1 |
| 2 |
| CE |
| AB |
0
0
．分析：在等腰三角形ABC中，底边BC=2，因此可取BC的中点O作为坐标原点距离平面直角坐标系．利用向量的坐标运算解决共线与数量积即可得出答案．
解答：解：∵在等腰三角形ABC中，底边BC=2，∴可取BC的中点O作为坐标原点距离平面直角坐标系．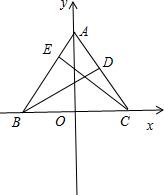
则B（-1，0），C（1，0），
设A（0，a）（a＞0）．∵
=
，∴D(
，
)．
∴
=(
，
)，
=（1，-a）．
∵
•
=
，∴
-
=
，解得a=
．
∴A(0，
)．
∵
=
，∴
=
，∴
=
+
=(0，
)+
(-1，-
)=(-
，
)．
∴
=(-
，
)．
∴
•
=(-
，
)•(-1，-
)=
-
=0．
故答案为0．
则B（-1，0），C（1，0），
设A（0，a）（a＞0）．∵
| AD |
| DC |
| 1 |
| 2 |
| a |
| 2 |
∴
| BD |
| 3 |
| 2 |
| a |
| 2 |
| AC |
∵
| BD |
| AC |
| 1 |
| 2 |
| 3 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
| 2 |
∴A(0，
| 2 |
∵
| AE |
| 1 |
| 2 |
| EB |
| AE |
| 1 |
| 3 |
| AB |
| OE |
| OA |
| 1 |
| 3 |
| AB |
| 2 |
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
2
| ||
| 3 |
∴
| CE |
| 4 |
| 3 |
2
| ||
| 3 |
∴
| CE |
| AB |
| 4 |
| 3 |
2
| ||
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
故答案为0．
点评：熟练掌握通过建立平面直角坐标系，利用向量的坐标运算解决共线和数量积是解题的关键．
练习册系列答案
相关题目