题目内容
4.在棱长为a的正方体ABCD-A1B1C1D1中,E,F分别为DD1和BB1的中点.(1)求证:AEC1F是平行四边形;
(2)求AE和AF之间的夹角的余弦值;
(3)求四边形AEC1F的面积.
分析 (1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,求出$\overrightarrow{AE}=\overrightarrow{F{C}_{1}}$,由此能证明AEC1F是平行四边形.
(2)求出$\overrightarrow{AE}$=(-a,0,$\frac{a}{2}$),$\overrightarrow{AF}$=(0,a,$\frac{a}{2}$),由此利用向量法能求出AE和AF之间的夹角的余弦值.
(3)四边形AEC1F的面积S=2S△AEF=2×2×$|\overrightarrow{AE}|×|\overrightarrow{AF}|$×$sin<\overrightarrow{AE},\overrightarrow{AF}>$,由此利用向量法能求出结果.
解答 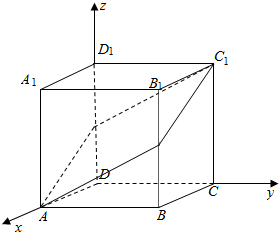 (1)证明:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
(1)证明:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
由已知得A(a,0,0),E(0,0,$\frac{a}{2}$),F(a,a,$\frac{a}{2}$),C1(0,a,a),
$\overrightarrow{AE}$=(-a,0,$\frac{a}{2}$),$\overrightarrow{F{C}_{1}}$=(-a,0,$\frac{a}{2}$),
∴$\overrightarrow{AE}=\overrightarrow{F{C}_{1}}$,∴AE$\underset{∥}{=}$FC1,
∴AEC1F是平行四边形.
(2)解:设AE和AF之间的夹角为θ,
∵$\overrightarrow{AE}$=(-a,0,$\frac{a}{2}$),$\overrightarrow{AF}$=(0,a,$\frac{a}{2}$),
∴cosθ=|$\frac{\overrightarrow{AE}•\overrightarrow{AF}}{|\overrightarrow{AE}|•|\overrightarrow{AF}|}$|=|$\frac{\frac{{a}^{2}}{4}}{\sqrt{{a}^{2}+\frac{{a}^{2}}{4}•\sqrt{{a}^{2}+\frac{{a}^{2}}{4}}}}$|=$\frac{1}{5}$,
∴AE和AF之间的夹角的余弦值为$\frac{1}{5}$.
(3)sin<$\overrightarrow{AE},\overrightarrow{AF}$>=sinθ=$\sqrt{1-(\frac{1}{5})^{2}}$=$\frac{2\sqrt{6}}{5}$,
∴四边形AEC1F的面积:
S=2S△AEF=2×2×$|\overrightarrow{AE}|×|\overrightarrow{AF}|$×$sin<\overrightarrow{AE},\overrightarrow{AF}>$
=4×$\frac{5}{4}{a}^{2}$×$\frac{2\sqrt{6}}{5}$
=2$\sqrt{6}{a}^{2}$.
点评 本题考查平行四边形的证明,考查两异面直线的夹角的余弦值的求法,考查平行四边形面积的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | -1 |
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{9}$ |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 30° | B. | 90° | C. | 120° | D. | 60° |