题目内容
【题目】已知
是椭圆
的左、右焦点，离心率为
，
是平面内两点，满足
，线段
的中点
在椭圆上，
周长为12.
（1）求椭圆
的方程；
（2）若与圆
相切的直线
与椭圆交于
，求
（其中
为坐标原点）的取值范围.
【答案】（1）
（2）
【解析】
（1）由已知可得
是线段
的中点，再由
是线段
的中点，结合椭圆定义可得
周为
，再由离心率，求出
，即可求出椭圆标准方程.
（2）先考虑直线
斜率不存在，求出
，直线斜率存在，设直线方程
，与单位圆相切求出
关系，直线方程与椭圆方程联立，消去
，求出
横坐标乘积，进而求出纵坐标乘积，结合关系，求出关于
目标函数，根据函数的特点，求出其范围.
（1）连接
，
，
，
是线段的中点，
是线段的中点，
由椭圆的定义知，
，
周长为
，
由离心率为
知，
，解得
，
，
椭圆
的方程为
.()
（2）当直线的斜率不存在时，直线
，
代入椭圆方程解得
，此时
，
当直线的斜率存在时，设直线的方程为，
由直线与圆
相切知，
，
，
将直线方程代入椭圆的方程
整理得，
，
设
，则
，
，
，
，
，
，
，
，
，
综上所述，的取值范围为
.
【题目】同程旅游随机调查了年龄在
（单位：岁）内的1250人的购票情况，其中50岁以下（不包含50岁）的有900人，50岁以上（包含50岁）的有350人，由调查数据的统计结果显示，有
的人参与网上购票，网上购票人数的频率分布直方图如下图所示.
（1）已知年龄在
，
，
的网上购票人数成等差数列，求
的值；
（2）根据题目数据填写
列联表，并根据填写数据判断能否在犯错误的概率不超过0.001的前提下，认为网上购票与年龄有关系？
50岁以下 | 50岁以上 | 总计 | |
参与网上购票 | |||
不参与网上购票 | |||
总计 |
附：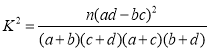
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
（3）为鼓励大家网上购票，该平台常采用购票就发放酒店入住代金券的方法进行促销，具体做法如下：年龄在
岁的每人发放20元，其余年龄段的每人发放50元，先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取10人，并在这10人中随机抽取3人进行回访调查，求此3人获得代金券的金额总和
的分布列和数学期望.
