题目内容
【题目】已知圆C:
.
（1）若圆C的切线在x轴和y轴上的截距相等，且截距不为零，求此切线的方程；
（2）从圆C外一点P
向该圆引一条切线，切点为M，O为坐标原点，且有
，
求使得
取得最小值的点P的坐标
【答案】（1）x＋y＋1＝0或x＋y－3＝0；（2）点P的坐标为
.
【解析】
本题考查用点斜式、斜截式求直线方程的方法，体现了分类讨论的数学思想，点到直线的距离公式，判断P在直线2x-4y+3=0上，|PM|的最小值就是|PO|的最小值，时间诶体的关键．
（1）当截距不为零时：设切线方程为
，根据圆心到切线的距离等于半径求出a的值，即得切线方程，当截距等于零时：设切线方程为y=kx（k≠0），同理可得k=2±
，从而得到圆的所有的切线方程．
（2）有切线的性质可得|PM|2=|PC|2-|CM|2，又|PM|=|PO|，可得2x0-4y0+3=0．动点P在直线2x-4y+3=0上，|PM|的最小值就是|PO|的最小值，过点O作直线2x-4y+3=0的垂线，垂足为P，垂足坐标即为所求．
（1）
切线在两坐标轴上的截距相等且截距不为零，
设切线方程为
，（
）
又圆C：
，圆心C
到切线的距离等于圆的半
径
， 
则所求切线的方程为：
。
（2）切线PM与半径CM垂直， 
动点P的轨迹是直线
，
的最小值就是
的最小
值，而的最小值为O到直线的距离d=
，
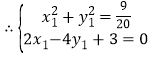
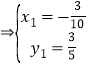
所求点坐标为P
.
练习册系列答案
口算能手系列答案
相关题目
