题目内容
如图，在四棱锥P－ABCD中，PA⊥底面ABCD，AB⊥CD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．
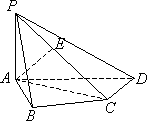
(Ⅰ)求PB和平面PAD所成的角的大小；
(Ⅱ)证明AE⊥平面PCD；
(Ⅲ)求二面角A－PD－C的大小．
答案：
解析：
解析：
|
(Ⅰ)解：在四棱锥 又 在 所以 (Ⅱ)证明：在四棱锥 因 由条件 又 由 (Ⅲ)解：过点 因此 由已知，可得 在 在 所以二面角 |
中，因
底面
，
平面
，故
．
，
，从而
平面
．故
在平面
内的射影为
，从而
为
和平面
所成的角．
中，
，故
．
和平面
所成的角的大小为
．
中，
底面
，
平面
，故
．
，
，
面
．
面
，
．
，
，可得
．
是
的中点，
，
．综上得
平面
．
作
，垂足为
，连结
．由(Ⅱ)知，
平面
，
在平面
内的射影是
，则
．
是二面角
的平面角．
．设
，可得
，
，
，
．
中，
，
，则
．
中，
．
的大小
．
练习册系列答案
相关题目
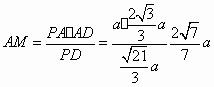如图，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，且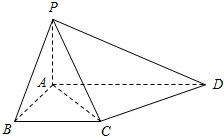
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，且AD∥BC，∠ABC=∠PAD=
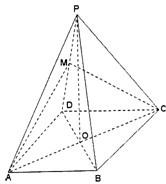如图，在四棱锥P-ABCD中，底面ABCD为等腰梯形，AB∥CD，AD=BC=2，对角线AC⊥BD于O，∠DAO=60°，且PO⊥平面ABCD，直线PA与底面ABCD所成的角为60°，M为PD上的一点．
如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E，F分别是AB，PB的中点．