题目内容
如图1,在平面内,ABCD边长为2的正方形,ADD″A1和CDD″C1都是正方形.将两个正方形分别沿AD,CD折起,使D″与D′重合于点D1.设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设BE=t(t>0)(图2).(1)设二面角E-AC-D1的大小为θ,当t=2时,求θ的余弦值;
(2)当t>2时在线段D1E上是否存在点P,使平面PA1C1∥平面EAC,若存在,求出P分
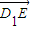 所成的比λ;若不存在,请说明理由.
所成的比λ;若不存在,请说明理由.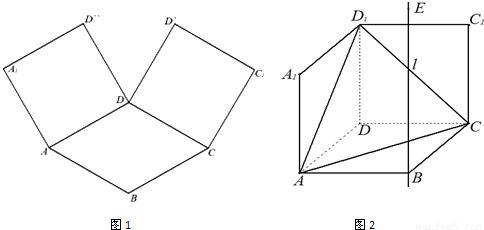
【答案】分析:(1)先找到二面角E-AC-D1的平面角,由余弦定理,求出平面角的余弦值,即可.
(2)先假设存在点P,使平面PA1C1∥平面EAC,建立空间直角坐标系,找到平面ACE的法向量,根据P分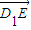 所成的比为λ,得
所成的比为λ,得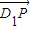 =
=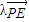 ,计算出λ的值,若能算出,则存在,若计算不出,则不存在.
,计算出λ的值,若能算出,则存在,若计算不出,则不存在.
解答:解:(1)连接DB交AC于点O,连接DO,EO,在△ADC中,DO⊥AC,
同理可证,EO⊥AC
∴∠D1OE为所求二面角的平面角θ
在△ADC中,∵AD1=CD1=AC=2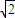 ,∴OD1=
,∴OD1=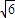
同理可得,OE=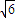 ,又∵D1E=2
,又∵D1E=2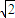
∴在△D1OE中,由余弦定理得,cosθ=
(2)设以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.BE=t
则,D(0,0,0),A(2,0,0),C(2,2,0),A1(2,0,2),D1(0,0,2),C1(0,2,2),E(2,2,t0
假设粗在满足题意的点P(x,y,z)
∵P分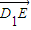 所成的比为λ,∴
所成的比为λ,∴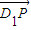 =
=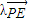 ?(x,y,z)=λ(2-x,2-y,t-z)
?(x,y,z)=λ(2-x,2-y,t-z)
解得,x=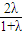 ,y=
,y=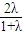 ,z=
,z=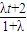
P(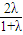 ,
,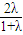 ,
,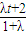 )
)
∴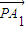 =(
=(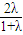 ,
,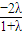 ,
,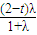 )
)
设平面ACE的法向量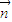 =(x,y,z)
=(x,y,z)
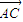 =(-2,2,0),
=(-2,2,0),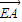 =(0,-2,-t)
=(0,-2,-t)
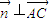 ?-2x+2y=0,
?-2x+2y=0,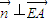 ?-2y-ty=0
?-2y-ty=0
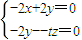 ⇒
⇒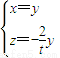
令x0=y0=t,则,z0=-2,∴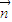 =(t,t,-2)
=(t,t,-2)
平面PA1C1∥平面EAC,得PA1∥平面EAC
∴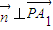 ?
?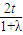 -
-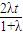 -
-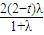 =0⇒λ=
=0⇒λ=
∴在线段D1E上是存在点P,使平面PA1C1∥平面EAC,P分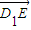 所成的比λ=
所成的比λ= (t>2)
(t>2)
点评:本题考查了二面角的平面角的求法,以及用空间向量判断立体几何位置关系.
(2)先假设存在点P,使平面PA1C1∥平面EAC,建立空间直角坐标系,找到平面ACE的法向量,根据P分
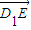 所成的比为λ,得
所成的比为λ,得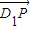 =
=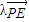 ,计算出λ的值,若能算出,则存在,若计算不出,则不存在.
,计算出λ的值,若能算出,则存在,若计算不出,则不存在.解答:解:(1)连接DB交AC于点O,连接DO,EO,在△ADC中,DO⊥AC,
同理可证,EO⊥AC
∴∠D1OE为所求二面角的平面角θ
在△ADC中,∵AD1=CD1=AC=2
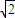 ,∴OD1=
,∴OD1=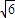
同理可得,OE=
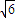 ,又∵D1E=2
,又∵D1E=2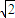
∴在△D1OE中,由余弦定理得,cosθ=

(2)设以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.BE=t
则,D(0,0,0),A(2,0,0),C(2,2,0),A1(2,0,2),D1(0,0,2),C1(0,2,2),E(2,2,t0
假设粗在满足题意的点P(x,y,z)
∵P分
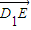 所成的比为λ,∴
所成的比为λ,∴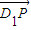 =
=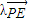 ?(x,y,z)=λ(2-x,2-y,t-z)
?(x,y,z)=λ(2-x,2-y,t-z)解得,x=
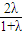 ,y=
,y=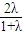 ,z=
,z=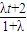
P(
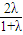 ,
,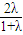 ,
,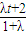 )
)∴
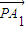 =(
=(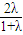 ,
,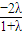 ,
,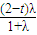 )
)设平面ACE的法向量
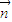 =(x,y,z)
=(x,y,z)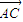 =(-2,2,0),
=(-2,2,0),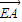 =(0,-2,-t)
=(0,-2,-t)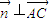 ?-2x+2y=0,
?-2x+2y=0,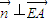 ?-2y-ty=0
?-2y-ty=0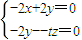 ⇒
⇒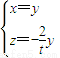
令x0=y0=t,则,z0=-2,∴
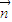 =(t,t,-2)
=(t,t,-2)平面PA1C1∥平面EAC,得PA1∥平面EAC
∴
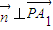 ?
?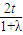 -
-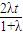 -
-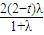 =0⇒λ=
=0⇒λ=
∴在线段D1E上是存在点P,使平面PA1C1∥平面EAC,P分
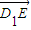 所成的比λ=
所成的比λ= (t>2)
(t>2)点评:本题考查了二面角的平面角的求法,以及用空间向量判断立体几何位置关系.

练习册系列答案
相关题目
己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
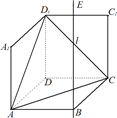 如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).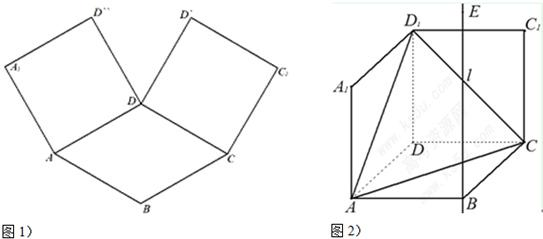
 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).

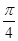 £ q £
£ q £  ,求线段BE长的取值范围;
,求线段BE长的取值范围; 上存在点
上存在点 ,使平面
,使平面 平面
平面 ,求
,求 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有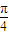 ≤θ≤
≤θ≤ ,求线段BE长的取值范围;
,求线段BE长的取值范围; 与BE之间满足的关系式,并证明:当0<BE<a时,恒有
与BE之间满足的关系式,并证明:当0<BE<a时,恒有 <1.
<1.