题目内容
(本题满分14分)
如图1,在平面内,ABCD是 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).


(Ⅰ) 设二面角E – AC – D1的大小为q,若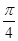 £ q £
£ q £  ,求线段BE长的取值范围;
,求线段BE长的取值范围;
(Ⅱ)在线段 上存在点
上存在点 ,使平面
,使平面 平面
平面 ,求
,求 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有 <
1.
<
1.
(方法1)设菱形 的中心为O,以O为原点,对角线AC,BD所在直线分别为x,y轴,建立空间直角坐标系如图1.设BE = t (t > 0) .
的中心为O,以O为原点,对角线AC,BD所在直线分别为x,y轴,建立空间直角坐标系如图1.设BE = t (t > 0) .

(Ⅰ)
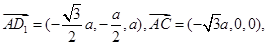
设平面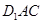 的法向量为
的法向量为 ,则
,则
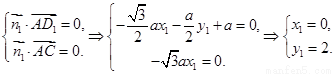
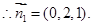 3分
3分
 设平面
设平面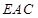 的法向量为
的法向量为 ,
,
则
 4分
4分
设二面角 的大小为
的大小为 ,则
,则 , 6分
, 6分
∵cosq Î , ∴
, ∴

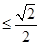 ,
,
解得  £ t £
£ t £  . 所以BE的取值范围是
[
. 所以BE的取值范围是
[ ,
, ]. 8分
]. 8分
(Ⅱ) 设 ,则
,则

由平面 平面
平面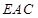 ,得
,得 平面
平面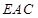 ,
,
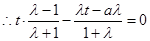 ,化简得:
,化简得: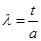 (t ¹ a),即所求关系式:
(t ¹ a),即所求关系式: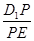
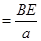 (BE ¹ a).
(BE ¹ a).
∴当0< t < a时,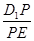 < 1. 即:当0 < BE < a时,恒有
< 1. 即:当0 < BE < a时,恒有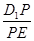 < 1.
14分
< 1.
14分
(方法2)
(Ⅰ)如图2,连接D1A,D1C,EA,EC,D1O,EO,
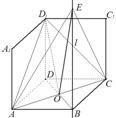
∵ D1A= D1C,所以,D1O⊥AC,同理,EO⊥AC,
∴ 是二面角
是二面角 的平面角.设其为q. 3分
的平面角.设其为q. 3分
连接D1E,在△OD1E中,设BE = t (t > 0)则有:
OD1
=  ,OE =
,OE =  ,D1E =
,D1E =  ,
,
∴  .
6分
.
6分
∵cosq Î , ∴
, ∴

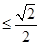 ,
,
解得  £ t £
£ t £  . 所以BE的取值范围是
[
. 所以BE的取值范围是
[ ,
, ].
].
所以当条件满足时, £ BE £
£ BE £  .
8分
.
8分
(Ⅱ)当点E在平面A1D1C1上方时,连接A1C1,则A1C1∥AC,

连接EA1,EC1,设A1C1的中点为O1,则O1在平面BDD1内,过O1作O1P∥OE交D1E于点P,则平面 平面
平面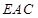 .
.
作平面BDD1如图3.过D1作D1B1∥BD交于l点B1,设EO交D1B1于点Q.
因为O1P∥OE,所以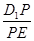 =
= =
= ,
,
由Rt△EB1Q∽RtEBO,得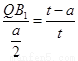 ,解得QB1 =
,解得QB1 = 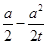 ,得
,得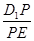 =
= , 12分
, 12分
当点E在平面A1D1C1下方时,同理可得,上述结果仍然成立. 13分
∴有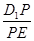 =
= (BE ¹a),∴当0 < t < a时,
(BE ¹a),∴当0 < t < a时,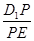 <
1. 14分
<
1. 14分
【解析】略

 阅读快车系列答案
阅读快车系列答案 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).