题目内容
已知函数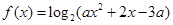 ,
,
(Ⅰ)当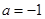 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;
(Ⅱ)如果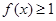 在区间
在区间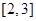 上恒成立,求实数
上恒成立,求实数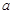 的取值范围.
的取值范围.
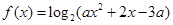 ,
,(Ⅰ)当
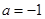 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;(Ⅱ)如果
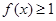 在区间
在区间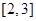 上恒成立,求实数
上恒成立,求实数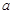 的取值范围.
的取值范围.解:(1) 当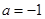 时,
时,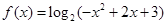
令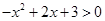 ,解得
,解得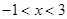
所以函数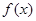 的定义域为
的定义域为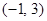 .
.
令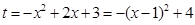 ,则
,则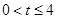
所以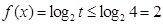
因此函数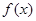 的值域为
的值域为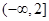 6分
6分
(2) 解法一: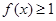 在区间
在区间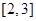 上恒成立等价于
上恒成立等价于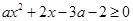 在区间
在区间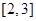 上恒成立
上恒成立
令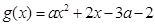
当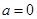 时,
时,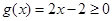 ,所以
,所以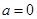 满足题意.
满足题意.
当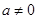 时,
时,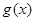 是二次函数,对称轴为
是二次函数,对称轴为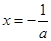 ,
,
当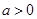 时,
时,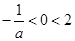 ,函数
,函数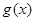 在区间
在区间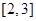 上是增函数,
上是增函数,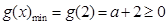 ,解得
,解得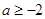 ;
;
当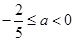 时,
时,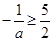 ,
,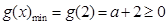 ,解得
,解得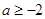
当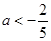 时,
时,
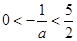 ,
,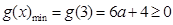 ,解得
,解得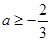
综上,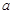 的取值范围是
的取值范围是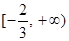 12分
12分
解法二: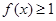 在区间
在区间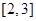 上恒成立等价于
上恒成立等价于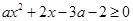 在区间
在区间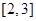 上恒成立
上恒成立
由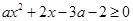 且
且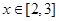 时,
时,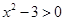 ,得
,得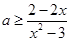
令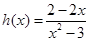 ,则
,则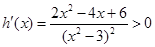
所以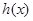 在区间
在区间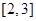 上是增函数,所以
上是增函数,所以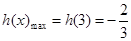
因此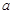 的取值范围是
的取值范围是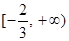 . 12分
. 12分
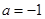 时,
时,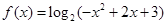
令
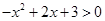 ,解得
,解得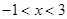
所以函数
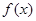 的定义域为
的定义域为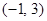 .
.令
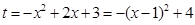 ,则
,则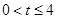
所以
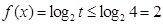
因此函数
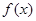 的值域为
的值域为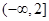 6分
6分(2) 解法一:
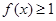 在区间
在区间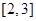 上恒成立等价于
上恒成立等价于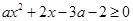 在区间
在区间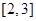 上恒成立
上恒成立令
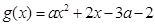
当
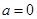 时,
时,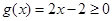 ,所以
,所以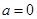 满足题意.
满足题意.当
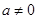 时,
时,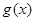 是二次函数,对称轴为
是二次函数,对称轴为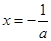 ,
,当
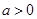 时,
时,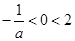 ,函数
,函数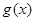 在区间
在区间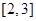 上是增函数,
上是增函数,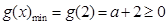 ,解得
,解得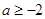 ;
;当
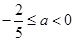 时,
时,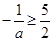 ,
,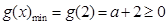 ,解得
,解得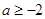
当
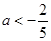 时,
时,
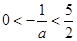 ,
,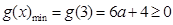 ,解得
,解得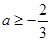
综上,
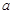 的取值范围是
的取值范围是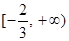 12分
12分解法二:
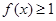 在区间
在区间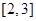 上恒成立等价于
上恒成立等价于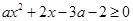 在区间
在区间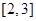 上恒成立
上恒成立由
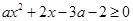 且
且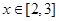 时,
时,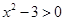 ,得
,得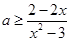
令
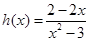 ,则
,则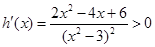
所以
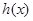 在区间
在区间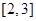 上是增函数,所以
上是增函数,所以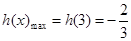
因此
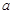 的取值范围是
的取值范围是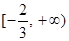 . 12分
. 12分略

练习册系列答案
相关题目
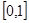 的函数
的函数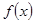 同时满足以下三个条件:
同时满足以下三个条件: ,总有
,总有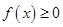 ;
;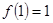 ;
;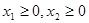 且
且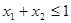 ,则有
,则有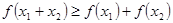 成立,则称
成立,则称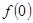 的值;
的值;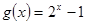 在区间
在区间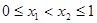 ,求证:
,求证: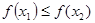 。
。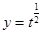 (B)
(B) (C)
(C)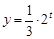 (D)
(D) 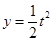
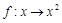 是集合A到B的映射,如果B={1,2},则A∩B只可能是
是集合A到B的映射,如果B={1,2},则A∩B只可能是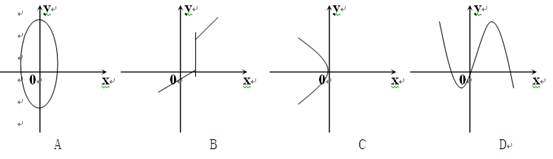
 的定义域为
的定义域为 ,若
,若
 ,
, ,则
,则 ( )
( )



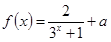 的零点为1,则实数a的值为( )
的零点为1,则实数a的值为( )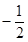 C.
C.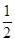 D.2
D.2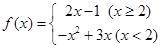 ,则
,则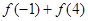 的值为( )
的值为( )