Question

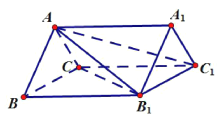
【题目】已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且 =λ（0＜λ＜1）．

（Ⅰ）求证：不论λ为何值，总有平面BEF⊥平面ABC；
（Ⅱ）当λ为何值时，平面BEF⊥平面ACD？

Answer 1

【答案】证明：（Ⅰ）∵AB⊥平面BCD，∴AB⊥CD，

∵CD⊥BC且AB∩BC=B，∴CD⊥平面ABC．

又∵ ，

∴不论λ为何值，恒有EF∥CD，∴EF⊥平面ABC，EF平面BEF，

∴不论λ为何值恒有平面BEF⊥平面ABC．

（Ⅱ）由（Ⅰ）知，BE⊥EF，又∵平面BEF⊥平面ACD，

∴BE⊥平面ACD，∴BE⊥AC．

∵BC=CD=1，∠BCD=90°，∠ADB=60°，

∴ ，（11分）

∴ ，

由AB2=AEAC得 ，∴ ，

故当 时，平面BEF⊥平面ACD．

【解析】（Ⅰ）根据线面垂直的判定定理可得证CD⊥平面ABC，利用已知可得对应边成比例可得EF∥CD进而可得EF⊥平面ABC根据面面垂直的判定定理可得证平面BEF⊥平面ABC（Ⅱ）利用面面垂直的性质定理可得证BE⊥平面ACD进而得出BE⊥AC，在三角形BCD和三角形ABD中由已知可解得AC 、AE的值，故可求出 λ的值使得平面BEF⊥平面ACD。
【考点精析】通过灵活运用直线与平面垂直的性质和平面与平面垂直的判定，掌握垂直于同一个平面的两条直线平行；一个平面过另一个平面的垂线，则这两个平面垂直即可以解答此题．