题目内容
为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
从第—个车主开始预约登记时计时(用频率估计概率),
(l)估计第三个车主恰好等待4分钟开始登记的概率:
(2)X表示至第2分钟末已登记完的车主人数,求X的分布列及数学期望.
| 登记所需时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(l)估计第三个车主恰好等待4分钟开始登记的概率:
(2)X表示至第2分钟末已登记完的车主人数,求X的分布列及数学期望.
(l)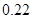 (2)
(2)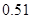
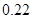 (2)
(2)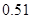
试题分析:解:设Y表示车主登记所需的时间,用频率估计概率,Y的分布如下:
| Y | 1 | 2 | 3 | 4 | 5 |
| P | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(1)第一个车主登记所需时间为1分钟,且第二个车主登记所需的时间为3分钟;
(2)第一个车主登记所需的时间为3分钟,且第二个车主登记所需的时间为1分钟;
(3)第一个和第二个车主登记所需的时间均为2分钟。
所以
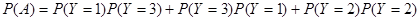
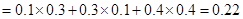
(2)X所有可能的取值为:0,1,2.X=0对应第一个车主登记所需的时间超过2分钟,所
以
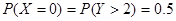 ;X=1对应第一个车主登记所需的时间为1分钟且
;X=1对应第一个车主登记所需的时间为1分钟且第二个车主登记所需时间超过1分钟,或第一个车主登记所需的时间为2分钟,
所以
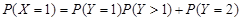
 ;X=2对应两个
;X=2对应两个车主登记所需的时间均为1分钟,所以
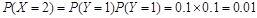 ;
;所以X的分布列为
| X | 0 | 1 | 2 |
| P | 0.5 | 0.49 | 0.01 |
 . 12分
. 12分点评:本题考查概率的求解,考查离散型随机变量的分布列与期望,解题的关键是明确变量的取值与含义.

练习册系列答案
相关题目
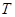 (单位:年)有关,若
(单位:年)有关,若 ,则销售利润为0元;若
,则销售利润为0元;若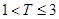 ,则销售利润为100元,若
,则销售利润为100元,若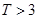 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间 ,又知
,又知 为方程
为方程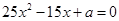 的两根,且
的两根,且 .
.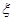 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记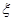 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求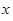 的分布列及期望。
的分布列及期望。
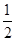
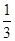

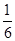
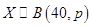 ,且
,且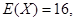 则
则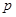 等于( )
等于( )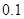
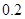
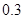
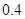
 中,当解释变量 x 每增加一个单位时,预报变量
中,当解释变量 x 每增加一个单位时,预报变量 增加0.1个单位 ( )
增加0.1个单位 ( )