题目内容
某种家用电器每台的销售利润与该电器的无故障时间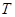 (单位:年)有关,若
(单位:年)有关,若 ,则销售利润为0元;若
,则销售利润为0元;若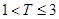 ,则销售利润为100元,若
,则销售利润为100元,若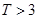 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间 ,
,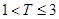 ,
,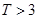 这三种情况发生的概率分别为
这三种情况发生的概率分别为 ,又知
,又知 为方程
为方程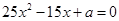 的两根,且
的两根,且 .
.
(1)求 的值;
的值;
(2)记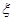 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求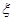 的分布列及数学期望.
的分布列及数学期望.
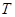 (单位:年)有关,若
(单位:年)有关,若 ,则销售利润为0元;若
,则销售利润为0元;若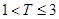 ,则销售利润为100元,若
,则销售利润为100元,若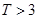 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间 ,
,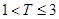 ,
,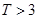 这三种情况发生的概率分别为
这三种情况发生的概率分别为 ,又知
,又知 为方程
为方程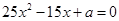 的两根,且
的两根,且 .
.(1)求
 的值;
的值;(2)记
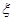 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求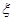 的分布列及数学期望.
的分布列及数学期望.(Ⅰ) 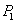 =
= ,
, =
=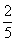 ,
,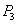 =
=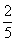 .
.
(Ⅱ)随机变量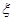 的分布列为
的分布列为
所求的数学期望为E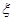 =0
=0
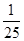 +100
+100
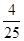 +200
+200
 +300
+300
 +400
+400
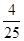 =240(元)
=240(元)
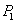 =
= ,
, =
=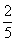 ,
,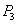 =
=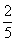 .
. (Ⅱ)随机变量
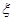 的分布列为
的分布列为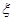 | 0 | 100 | 200 | 300 | 400 |
| p | 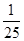 | 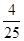 |  |  | 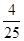 |
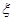 =0
=0
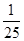 +100
+100
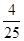 +200
+200
 +300
+300
 +400
+400
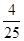 =240(元)
=240(元)试题分析:(Ⅰ)由已知得 :

解得:
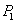 =
= ,
, =
=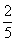 ,
,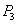 =
=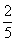 .
. (Ⅱ)
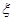 的可能取值为0,100,200,300,400.
的可能取值为0,100,200,300,400. P(
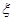 ="0)="
="0)=" 

 =
=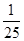 P(
P(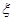 ="100)=" 2
="100)=" 2


 =
=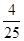
P(
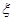 ="200)=" 2
="200)=" 2


 +
+

 =
= P(
P(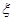 ="300)=" 2
="300)=" 2


 =
=
P(
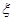 ="400)="
="400)=" 

 =
=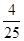
随机变量
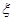 的分布列为
的分布列为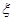 | 0 | 100 | 200 | 300 | 400 |
| p | 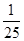 | 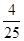 |  |  | 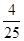 |
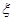 =0
=0
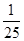 +100
+100
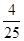 +200
+200
 +300
+300
 +400
+400
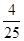 =240(元)
=240(元)点评:中档题,近些年的高考题中,概率统计问题,往往以应用题出现。确定随机变量的分布列,关键是计算事件的概率。

练习册系列答案
相关题目


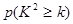
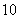 个编号为
个编号为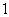 、
、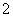 、
、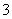 的球,
的球,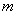 个,
个,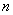 个.从袋中依次摸出
个.从袋中依次摸出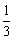 .
.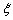 ,求随机变量
,求随机变量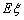 .
.
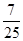
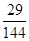
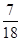








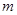

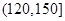





 分以上的人数;
分以上的人数;