题目内容
已知f(x)在R上是增函数,且f(k·3x)-f(9x-3x+2)<0对任意的x∈R都成立,求实数k的取值范围.
解:由已知f(k·3x)<f(9x-3x+2)对x∈R恒成立.
∵f(x)在R上是增函数,
∴只要k·3x<9x-3x+2对x∈R恒成立.
方法一:令t=3x,则t>0,上式等价于g(t)=t2-(k+1)t+2>0
对t∈(0,+∞)恒成立.
根据二次函数的图象性质得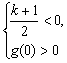 或
或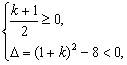
即![]() 或
或![]()
∴k<2![]() -1.
-1.
方法二:分离常数k得k<3x+![]() -1对一切x∈R恒成立.
-1对一切x∈R恒成立.
令h(x)=3x+![]() -1,只要k<h(x)的最小值.
-1,只要k<h(x)的最小值.
∵h(x)=3x+![]() -1≥2
-1≥2![]() -1=2
-1=2![]() -1,
-1,
∴h(x)的最小值为2![]() -1.
-1.
∴k<2![]() -1.
-1.
故所求k的取值范围是(-∞,2![]() -1).
-1).
点评:对于没有给出具体解析式的抽象函数f(x),如果知其单调性,就可以脱去函数值不等式中的函数符号;本题还充分说明了二次函数图象和性质的工具性作用;对于不等式恒成立问题,分离常数并构造函数求出其最值来确定常数取值范围不失为一个简单有效的方法.

练习册系列答案
相关题目
 ax2+3x+5(a>0).
ax2+3x+5(a>0).