题目内容
(本题满分12分)设函数f(x)=x3- ax2+3x+5(a>0).
ax2+3x+5(a>0).
(1)已知f(x)在R上是单调函数,求a的取值范围;
(2)若a=2,且当x∈[1,2]时,f(x)≤m恒成立,求实数m的取值范围.
【答案】
(1) 0<a≤6 ;(2) [15,+∞).
【解析】
试题分析:(1)f′(x)=3x2-ax+3, 2分
其判别式Δ=a2-36.
当0<a≤6时,f′(x)≥0恒成立, 4分
此时f(x)在R上为增函数. 6分
(2)a=2时,f′(x)=3x2-2x+3>0恒成立,
因此f(x)在(-∞,+∞)上是增函数, 8分
从而f(x)在[1,2]上递增,则f(x)max=f(2)=15, 10分
要使f(x)≤m在x∈[1,2]上恒成立,只需15≤m,
解得m∈[15,+∞).
故m的取值范围是[15,+∞). 12分
考点:利用导数研究函数的单调性。
点评:解决恒成立问题常用变量分离法,变量分离法主要通过两个基本思想解决恒成立问题, 思路1: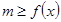 在
在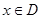 上恒成立
上恒成立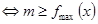 ;思路2:
;思路2: 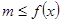 在
在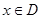 上恒成立
上恒成立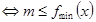 。
。

练习册系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;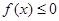 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求