题目内容
下列命题正确的是A.函数y=2x2+x+1在(0,+∞)上不是增函数
B.函数y=![]() 在(-∞,-1)∪(-1,+∞)上是函数
在(-∞,-1)∪(-1,+∞)上是函数
C.函数y=![]() (x2-4x-5)的单调增区间为(-∞,2)
(x2-4x-5)的单调增区间为(-∞,2)
D.已知f(x)在R上是增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b)
答案:D
【解析】函数y=2x2+x+1在[![]() ,+∞)上为增函数,即在(0,+∞)上必为增函数;
,+∞)上为增函数,即在(0,+∞)上必为增函数;
函数y=![]() 在定义域上不是减函数;函数y=
在定义域上不是减函数;函数y=![]() (x2-4x-5)的单调增区间为(-∞,-1).由此可得A、B、C均不正确.
(x2-4x-5)的单调增区间为(-∞,-1).由此可得A、B、C均不正确.
∵a+b>0,∴a>-b,b>-a,又f(x)为R上的增函数,∴f(a)>f(-b),f(b)>f(-a),即得f(a)+f(b)>f(-a)+f(-b).

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
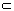 平面β,则下列命题正确的是
平面β,则下列命题正确的是  ,直线b
,直线b 直线a,b
直线a,b 平面
平面 ,则
,则
 则
则 B.若
B.若 , 则
, 则
 则
则 D.若
D.若