Question

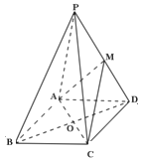
【题目】如图，已知在正四棱锥中， 为侧棱的中点， 连接相交于点。

（1）证明： ；

（2）证明： ；

（3）设,若质点从点沿平面与平面的表 面运动到点的最短路径恰好经过点，求正四棱锥 的体积。

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）.

【解析】试题分析：

（1）由中位线定理可得线线平面，从而有线面平行；

（2）正四棱锥中，底面是正方形，因此有，又PO是正四棱锥的高，从而有PO⊥AC，这样就有AC与平面PBD垂直，从而得面面垂直；

（3）把与沿PD摊平，由A、M、C共线，因此新的平面图形是平行四边形，从而为菱形，M到底面ABCD的距离为原正四棱锥高PO的一半，计算可得体积．

试题解析：

(1) 证明：连接OM，

∵O，M分别为BD，PD的中点，

∴在△PBD中，OM//PB，

又PB面ACM，OM面ACM，

∴ PB//面ACM

(2) 证明：连接PO.

∵在正四棱锥中，PA=PC，O为AC的中点，

∴PO⊥AC，BD⊥AC，

又PO∩BD=O， AC⊥平面PBD，

又 AC平面ACM，∴平面ACM ⊥平面PBD

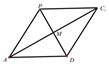
(3) 如图，把△PAD与 △PCD沿PD展开成平面四边形PADC1

由题意可知A，M，C1三点共线，

∵△PAD≌△PCD, M为PD的中点，

∴AM=MC1，即M为AC1中点，

∴平面四边形PADC1为平行四边形，

又PA= PC, ∴平面四边形PADC1为菱形，

∴正四棱锥的侧棱长为2

∵PO⊥AC，PO⊥BD，PO ⊥面ABCD，∴PO为正四棱锥的高