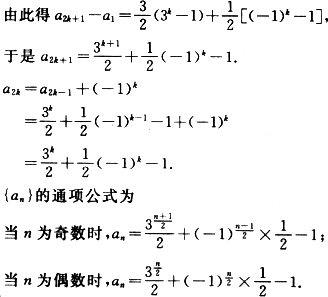Question

已知数列{a_n}中a₁＝1，且a_2k＝a_2k－1＋(－1)^k，a_2k+1＝a_2k＋3^k，其中k＝1，2，3，…．

(1)求a₃，a₅；

(2)求{a_n}的通项公式．

Answer 1

答案：
解析：

(1)a2＝a1＋(－1)1＝0， 　　a3＝a2＋31＝3， 　　a4＝a3＋(－1)2＝4， 　　a5＝a4＋32＝13， 　　∴a3＝3，a5＝13． 　　(2)a2k+1＝a2k＋3k 　　＝a2k－1＋(－1)k＋3k， 　　∴a2k+1－a2k－1＝3k＋(－1)k， 　　同理a2k－1－a2k－3＝3k－1＋(－1)k－1， 　　…… 　　a3－a1＝3＋(－1)． 　　∴(a2k+1－a2k－1)＋(a2k－1－a2k－3)＋…＋(a3－a1) 　　＝(3k＋3k－1＋…＋3)＋[(－1)k＋(－1)k－1＋…＋(－1)]，

提示：

重点考查数列的有关基础知识，考查分类讨论运算能力．求通项的关键是寻找项与项数之间的关系．