题目内容
已知数列{an}中,a1为由曲线y=
,直线y=x-2及y轴所围成图形的面积的
倍Sn为该数列的前n项和,且Sn+1=an(1-an+1)+Sn.
(1)求数列{an}的通项公式;
(2)若不等式an+an+1+an+2+…+a3n>
对一切正整数n都成立,求正整数a的最大值,并证明结论.
| x |
| 3 |
| 32 |
(1)求数列{an}的通项公式;
(2)若不等式an+an+1+an+2+…+a3n>
| a |
| 24 |
分析:(1)利用定积分可求得a1=
,再利用递推公式Sn+1=an(1-an+1)+Sn即可求得数列{an}的通项公式;
(2)当n=1时,
+
+
=
>
,于是a<26,据题意取a=25,用数学归纳法证明:
+
+…+
>
即可.
| 1 |
| 2 |
(2)当n=1时,
| 1 |
| 1+1 |
| 1 |
| 1+2 |
| 1 |
| 1+3 |
| 26 |
| 24 |
| a |
| 24 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n+1 |
| 25 |
| 24 |
解答:解:(1)依题意作图如下:
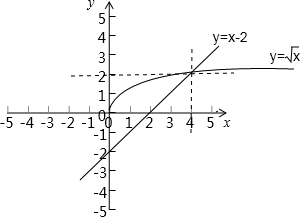
∵图中x轴下方的等腰直角三角形与x轴上方、直线x=4及直线y=x-2组成的等腰直角三角形全等,
∴a1=
dx=
×
x
|
=
,
∵Sn+1=an(1-an+1)+Sn,
∴an+1=an-an•an+1,
∴
-
=1,又a1=
,故
=2,
,∴{
}是首项为2,公差为1的等差数列,
∴
=2+(n-1)×1=n+1,
.∴an=
.
(2)当n=1时,
+
+
>
,即
>
,
所以a<26,而a是正整数,
所以取a=25,下面用数学归纳法证明:
+
+…+
>
.
(1)当n=1时,已证;
(2)假设当n=k时,不等式成立,即
+
+…+
>
.
则当n=k+1时,
有
+
+…+
=
+
+…+
+
+
+
-
>
+[
+
-
].
因为
+
=
>
,
所以
+
-
>0.
所以当n=k+1时不等式也成立.
由(1)(2)知,对一切正整数n,都有:
+
+…+
>
.
所以a的最大值等于25.

∵图中x轴下方的等腰直角三角形与x轴上方、直线x=4及直线y=x-2组成的等腰直角三角形全等,
∴a1=
| 3 |
| 32 |
| ∫ | 4 0 |
| x |
| 3 |
| 32 |
| 2 |
| 3 |
| 3 |
| 2 |
| | | 4 0 |
| 1 |
| 2 |
∵Sn+1=an(1-an+1)+Sn,
∴an+1=an-an•an+1,
∴
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| a1 |
,∴{
| 1 |
| an |
∴
| 1 |
| an |
.∴an=
| 1 |
| n+1 |
(2)当n=1时,
| 1 |
| 1+1 |
| 1 |
| 1+2 |
| 1 |
| 1+3 |
| a |
| 24 |
| 26 |
| 24 |
| a |
| 24 |
所以a<26,而a是正整数,
所以取a=25,下面用数学归纳法证明:
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n+1 |
| 25 |
| 24 |
(1)当n=1时,已证;
(2)假设当n=k时,不等式成立,即
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| 3k+1 |
| 25 |
| 24 |
则当n=k+1时,
有
| 1 |
| (k+1)+1 |
| 1 |
| (k+1)+2 |
| 1 |
| 3(k+1)+1 |
=
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| 3k+1 |
| 1 |
| 3k+2 |
| 1 |
| 3k+3 |
| 1 |
| 3k+4 |
| 1 |
| k+1 |
>
| 25 |
| 24 |
| 1 |
| 3k+2 |
| 1 |
| 3k+4 |
| 2 |
| 3(k+1) |
因为
| 1 |
| 3k+2 |
| 1 |
| 3k+4 |
| 6(k+1) |
| 9k2+18k+8 |
| 2 |
| 3(k+1) |
所以
| 1 |
| 3k+2 |
| 1 |
| 3k+4 |
| 2 |
| 3(k+1) |
所以当n=k+1时不等式也成立.
由(1)(2)知,对一切正整数n,都有:
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n+1 |
| 25 |
| 24 |
所以a的最大值等于25.
点评:本题考查数列递推式,考查数学归纳法,利用定积分求得a1=
是应用递推关系式Sn+1=an(1-an+1)+Sn的关键,通过数学归纳法的应用,考查推理证明的能力,属于难题.
| 1 |
| 2 |

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|