题目内容
在△ABC中,角A、B、C的对边分别为a,b,c,已知(b+c):(c+a):(a+b)=4:5:6,则下列结论正确的是______
(1)△ABC一定是钝角三角形;
(2)△ABC被唯一确定;
(3)sinA:sinB:sinC=7:5:3;
(4)若b+c=8,则△ABC的面积为
.
(1)△ABC一定是钝角三角形;
(2)△ABC被唯一确定;
(3)sinA:sinB:sinC=7:5:3;
(4)若b+c=8,则△ABC的面积为
15
| ||
| 2 |
在△ABC中,由于(b+c):(c+a):(a+b)=4:5:6,
可设b+c=4k,a+c=5k,a+b=6k,求得 a=
,b=
,c=
.
求得cosA=
=-
<0,故A=120°为钝角,故(1)正确.
由以上可得,三角形三边之比a:b:c=7:5:3,
故这样的三角形有无数多个,故(2)不正确,(3)正确.
若b+c=8,则b=5、c=3,由正弦定理可得
△ABC的面积为
bc•sinA=
×5×3×sin120°=
,故(4)不正确.
故答案为(1)、(3).
可设b+c=4k,a+c=5k,a+b=6k,求得 a=
| 7k |
| 2 |
| 5k |
| 2 |
| 3k |
| 2 |
求得cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
由以上可得,三角形三边之比a:b:c=7:5:3,
故这样的三角形有无数多个,故(2)不正确,(3)正确.
若b+c=8,则b=5、c=3,由正弦定理可得
△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
15
| ||
| 4 |
故答案为(1)、(3).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,则
,则 为( )
为( )

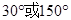


 中,若
中,若 ,则
,则 等于 ( )
等于 ( )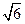 B
B C
C  D
D 