题目内容
在△ABC中,sin(A-B)+sinC=
,BC=
AC,则∠B=( )
| 3 |
| 2 |
| 3 |
A.
| B.
| C.
| D.
|
在△ABC中,∵sin(A-B)+sinC=
,
∴sin(A-B)+sin(A+B)=
,
∴2sinAcosB=
,
∴sinAcosB=
;①
∵BC=
AC,
∴a=
b,
∴由正弦定理得:sinA=
sinB;②
∴由①②得:
sinBcosB=
,
∴
sin2B=
,
∴sin2B=
,a=
b>b,故A>B,
∴2B=
,
∴B=
.
故选B.
| 3 |
| 2 |
∴sin(A-B)+sin(A+B)=
| 3 |
| 2 |
∴2sinAcosB=
| 3 |
| 2 |
∴sinAcosB=
| 3 |
| 4 |
∵BC=
| 3 |
∴a=
| 3 |
∴由正弦定理得:sinA=
| 3 |
∴由①②得:
| 3 |
| 3 |
| 4 |
∴
| ||
| 2 |
| 3 |
| 4 |
∴sin2B=
| ||
| 2 |
| 3 |
∴2B=
| π |
| 3 |
∴B=
| π |
| 6 |
故选B.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

 满足
满足 ,且
,且 与
与 的夹角为
的夹角为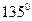 ,
, 与
与 ,
, ,则
,则 .
. 中,
中, = (结果用反三角函数值表示)
= (结果用反三角函数值表示)