题目内容
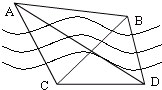
如图,隔河看两目标A、B,但不能到达,在岸边选取相距
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.

| 3 |

在△ACD中,∠ADC=30°,∠ACD=120°,∴∠CAD=30°.
∴AC=CD=
.
在△BDC中,∠CBD=180°-(45°+75°)=60°.
由正弦定理,得BC=
=
.
由余弦定理,得AB2=AC2+BC2-2AC•BC•cos∠BCA
=(
)2+(
)2-2
×
cos75°=5.
∴AB=
.
∴两目标A、B之间的距离为
km.
∴AC=CD=
| 3 |
在△BDC中,∠CBD=180°-(45°+75°)=60°.
由正弦定理,得BC=
| ||
| sin60° |
| ||||
| 2 |
由余弦定理,得AB2=AC2+BC2-2AC•BC•cos∠BCA
=(
| 3 |
| ||||
| 2 |
| 3 |
| ||||
| 2 |
∴AB=
| 5 |
∴两目标A、B之间的距离为
| 5 |


练习册系列答案
相关题目
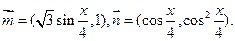
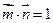 ,求
,求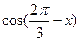 的值;
的值;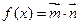 ,在
,在
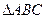 中,角
中,角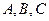 的对边分别是
的对边分别是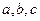 ,
,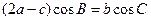 ,求函数
,求函数 的取值范围。
的取值范围。
 满足
满足 ,且
,且 与
与 的夹角为
的夹角为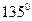 ,
, 与
与 ,
, ,则
,则 .
. 中,
中, 则BC =( )
则BC =( )


 ,
, ,则下列各式中正确的是( )
,则下列各式中正确的是( )


