题目内容
设△ABC的三内角A、B、C的对边长分别为a、b、c,已知bcosC=(2a-c)cosB.
(Ⅰ)求角B的大小;
(Ⅱ)若x∈[0,π),求函数f(x)=sin(x-B)+sinx的值域.
(Ⅰ)求角B的大小;
(Ⅱ)若x∈[0,π),求函数f(x)=sin(x-B)+sinx的值域.
(Ⅰ)由已知及正弦定理,得sinBcosC=(2sinA-sinC)cosB…(2分)
移项得sinBcosC+cosBsinC=2sinAcosB,
∴sin(B+C)=2sinAcosB…(4分)
∵sin(B+C)=sinA≠0,∴2cosB=1,可得cosB=
.(5分)
∵B∈(0,π),∴B=
…(6分)
(Ⅱ)∵B=
,
∴f(x)=sin(x-
)+sinx=sinxcos
-cosxsin
+sinx
=
sinx-
cosx=
sin(x-
)…(9分)
∵x∈[0,π),可得-
≤x-
<
,
∴sin(x-
)∈[-
,1]…(11分)
故函数f(x)的值域是[-
,
].(12分)
移项得sinBcosC+cosBsinC=2sinAcosB,
∴sin(B+C)=2sinAcosB…(4分)
∵sin(B+C)=sinA≠0,∴2cosB=1,可得cosB=
| 1 |
| 2 |
∵B∈(0,π),∴B=
| π |
| 3 |
(Ⅱ)∵B=
| π |
| 3 |
∴f(x)=sin(x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
∵x∈[0,π),可得-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(x-
| π |
| 6 |
| 1 |
| 2 |
故函数f(x)的值域是[-
| ||
| 2 |
| 3 |

练习册系列答案
相关题目
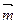 ="(sinA" ,sinB),
="(sinA" ,sinB),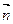 =(cosB,cosA),
=(cosB,cosA),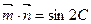 且A、B、C分别为△ABC的三边
且A、B、C分别为△ABC的三边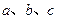 所对的角。
所对的角。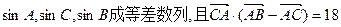 ,求c边的长。
,求c边的长。
 ,
, ,则下列各式中正确的是( )
,则下列各式中正确的是( )


