题目内容
设函数f (x)=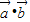 ,其中向量
,其中向量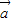 =(
=(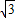 cosx,sinx),
cosx,sinx),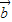 =(cosx,cosx).
=(cosx,cosx).①若函数y=sin2x按向量
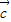 =(p,q) (|p|<
=(p,q) (|p|<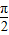 )平移后得到函数y=f (x)的图象,求实数p,q的值.
)平移后得到函数y=f (x)的图象,求实数p,q的值.②若f (x)=1+
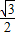 ,x∈[
,x∈[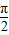 ,
,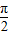 ],求sinx.
],求sinx.
【答案】分析:①先求出函数f (x)=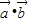 的表达式,利用二倍角公式和两角和的正弦函数,化简为f(x)=sin
的表达式,利用二倍角公式和两角和的正弦函数,化简为f(x)=sin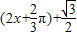 ,
,
根据平移求出向量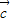 =(p,q),实数p,q的值.
=(p,q),实数p,q的值.
②利用f (x)=1+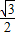 ,得到sin(2x+
,得到sin(2x+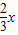 )=1,然后求出x的值,再求sinx.
)=1,然后求出x的值,再求sinx.
解答:解:①f(x)=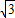 cos2x-sinxcosx=
cos2x-sinxcosx=
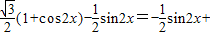
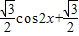
=sin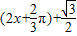
∴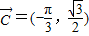 ,∴
,∴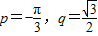 (6分)
(6分)
②sin(2x+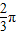 )+
)+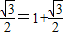
∴sin(2x+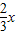 )=1
)=1
∴2x+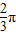 =
=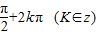
∴2x=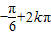 ,x=
,x=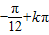 (k∈Z)
(k∈Z)
∵x∈[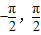 ],∴x=
],∴x=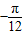 (10分)
(10分)
∴sin(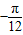 )=
)=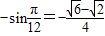 (12分)
(12分)
点评:本题是基础题,考查三角函数的化简,二倍角公式,两角和的正弦函数公式的应用,三角函数的图象的平移,简单三角方程的解法,考查计算能力.
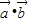 的表达式,利用二倍角公式和两角和的正弦函数,化简为f(x)=sin
的表达式,利用二倍角公式和两角和的正弦函数,化简为f(x)=sin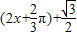 ,
,根据平移求出向量
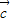 =(p,q),实数p,q的值.
=(p,q),实数p,q的值.②利用f (x)=1+
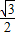 ,得到sin(2x+
,得到sin(2x+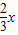 )=1,然后求出x的值,再求sinx.
)=1,然后求出x的值,再求sinx.解答:解:①f(x)=
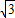 cos2x-sinxcosx=
cos2x-sinxcosx=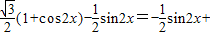
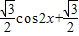
=sin
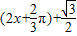
∴
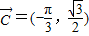 ,∴
,∴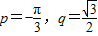 (6分)
(6分)②sin(2x+
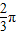 )+
)+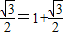
∴sin(2x+
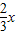 )=1
)=1∴2x+
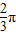 =
=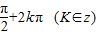
∴2x=
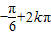 ,x=
,x=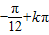 (k∈Z)
(k∈Z)∵x∈[
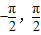 ],∴x=
],∴x=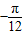 (10分)
(10分)∴sin(
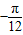 )=
)=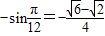 (12分)
(12分)点评:本题是基础题,考查三角函数的化简,二倍角公式,两角和的正弦函数公式的应用,三角函数的图象的平移,简单三角方程的解法,考查计算能力.

练习册系列答案
相关题目
 (2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
(2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )