题目内容
已知O是直角坐标原点，点A、B的坐标分别是（1，0），（0，1）．点P在线段AB上运动，设
与
的夹角为θ，则
•
关于θ的函数解析式
， θ∈[0 ，
]
， θ∈[0 ，
]．
| OA |
| OP |
| OA |
| OP |
| cosθ |
| cosθ+sinθ |
| π |
| 2 |
| cosθ |
| cosθ+sinθ |
| π |
| 2 |
分析：由题意可得
=
+λ
=（1-λ，λ），求得
•
=1-λ，由tanθ=
求出λ值，即可得到
•
的值．
| OP |
| OA |
| AB |
| OA |
| OP |
| λ |
| 1-λ |
| OA |
| OP |
解答：解：由题意可得
=
+λ
=（1，0）+λ （-1，1）=（1-λ，λ）．
∴
•
=（1，0）•（1-λ，λ）=1-λ．
又由题意可得 tanθ=
，∴λ=
．
∴
•
=1-λ=1-
=
，θ∈[0 ，
]．
故答案为：
， θ∈[0 ，
]．
| OP |
| OA |
| AB |
∴
| OA |
| OP |
又由题意可得 tanθ=
| λ |
| 1-λ |
| sinθ |
| cosθ+sinθ |
∴
| OA |
| OP |
| sinθ |
| cosθ+sinθ |
| cosθ |
| cosθ+sinθ |
| π |
| 2 |
故答案为：
| cosθ |
| cosθ+sinθ |
| π |
| 2 |
点评：本题主要考查两个向量的数量积公式，两个向量的加减法的法则及其几何意义，求出
•
=1-λ，tanθ=
是解题的关键．
| OA |
| OP |
| λ |
| 1-λ |
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
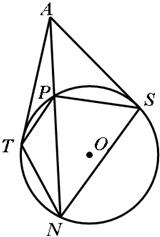选做题A．平面几何选讲
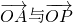的夹角为θ，则
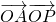关于θ的函数解析式________．
x，x > 0 }，点B∈{ ( x，y ) | y =