题目内容
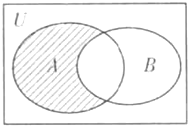（2013•韶关二模）设全集U=R，集合A={x|x（x+3）＜0}，B={x|x＜-1}，则如图中阴影部分表示的集合为（ ）
分析：根据题意，图中阴影部分表示的区域为只属于A的部分，即A∩（?UB），计算可得集合A与?UB，对其求交集可得答案．
解答：解：根据题意，图中阴影部分表示的区域为只属于A的部分，即A∩（?UB），
A={x|x（x+3）＜0}={x|-3＜x＜0}，
B={x|x＜-1}，则?UB={x|x≥-1}，
则A∩（?UB）={x|-1≤x＜0}，
故选B．
A={x|x（x+3）＜0}={x|-3＜x＜0}，
B={x|x＜-1}，则?UB={x|x≥-1}，
则A∩（?UB）={x|-1≤x＜0}，
故选B．
点评：本题考查集合的Venn表示法，关键是分析出阴影部分表示的集合．
练习册系列答案
计算高手系列答案
相关题目