题目内容
（2013•韶关二模）函数f(x)=lnx-
的零点的个数是（ ）
| 1 |
| x-1 |
分析：由于函数f（x）在定义域内不是连续的，所以并不能通过求导递增来直接判断零点的个数，利用数形结合法解决．
解答：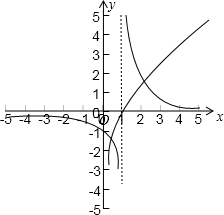
解：函数的定义域为（0，1）∪（1，+∞）
令f(x)=lnx-
=0，可知lnx=
分别画出函数y=lnx与y=
∴函数在（0，1）之间有一个零点，在x＞1有一个零点
故选B．
解：函数的定义域为（0，1）∪（1，+∞）令f(x)=lnx-
| 1 |
| x-1 |
| 1 |
| x-1 |
分别画出函数y=lnx与y=
| 1 |
| x-1 |
∴函数在（0，1）之间有一个零点，在x＞1有一个零点
故选B．
点评：本题考查函数的零点，考查数形结合思想的运用，应注意函数f（x）在定义域内不是连续的，所以并不能通过求导递增来直接判断零点的个数．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目