题目内容
【题目】设等差数列{an}的前n项和为Sn，若S9=81，a3+a5=14．
（1）求数列{an}的通项公式；
（2）设bn=
，若{bn}的前n项和为Tn，证明：Tn＜
．
【答案】（1）an=2n-1（2）证明见解析
【解析】
（1）根据等差数列的性质可知，S9=9a5=81，a3+a5=14，即可求出a3=5，a5=9，因而可求出公差
，故可求得通项公式．
（2）由
的形式可知，采用裂项相消法求出数列{bn}的前n项和，即可证明．
（1）设等差数列{an}的公差为d，
由S9=9a5=81，得a5=9，
又由a3+a5=14，得a3=5，
由上可得等差数列{an}的公差d
=2，
∴an=a3+（n-3）d=2n-1；
（2）由题意得，
.
所以
．
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
【题目】近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重. 大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查得到了如表所示的列联表:已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为
.
（1）请将列联表补充完整；
患心肺 疾病 | 不患心 肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
（2）是否有97.5%的把握认为患心肺疾病与性别有关?说明你的理由；
（3）已知在患心肺疾病的10位女性中，有3位又患胃病.现在从患心肺疾病的10位女性中，选出3名进行其他方面的排查，记选出患胃病的女性人数为
，求的分布列以及数学期望.下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式
，其中
）
【题目】大学先修课程，是在高中开设的具有大学水平的课程，旨在让学有余力的高中生早接受大学思维方式、学习方法的训练，为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年，共有250人参与学习先修课程.
（Ⅰ）这两年学校共培养出优等生150人，根据下图等高条形图，填写相应列联表，并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系？
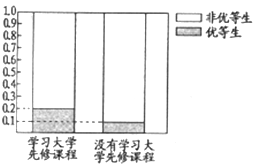
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
（Ⅱ）某班有5名优等生，其中有2名参加了大学生先修课程的学习，在这5名优等生中任选3人进行测试，求这3人中至少有1名参加了大学先修课程学习的概率.
参考数据：
| 0.15 | 0.10 | 0．05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式：
，其中
