题目内容
对某校高三年级学生参加社区服务次数进行统计, 随机抽取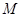 名学生作为样本,得到这
名学生作为样本,得到这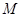 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
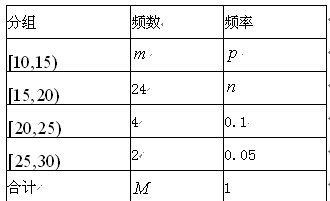
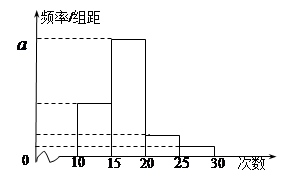
(Ⅰ)求出表中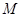 、
、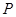 及图中
及图中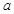 的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间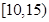 内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间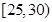 内的概率.
内的概率.
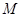 名学生作为样本,得到这
名学生作为样本,得到这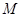 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: 

(Ⅰ)求出表中
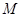 、
、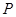 及图中
及图中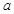 的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间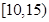 内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间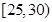 内的概率.
内的概率.(1)0.12;(2)60人;(3)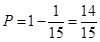
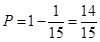
本试题主要是考查了频率分布直方图的运用。利用面积表示频率,得到参数的值,
然后结合古典概型概率公式得到概率的求解。
(1)中由分组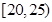 内的频数是4,频率是0.1,可知M的值和m的值
内的频数是4,频率是0.1,可知M的值和m的值
(2)因为该校高三学生有240人,分组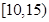 内的频率是0.25,从而得到人数为60人
内的频率是0.25,从而得到人数为60人
((3)利用在区间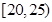 内的人为
内的人为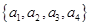 ,在区间
,在区间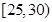 内的人为
内的人为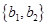 .
.
从中任意选两个人所有的基本事件数,得到事件A的基本事件数,运用概率公式得到。
解(Ⅰ)由分组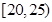 内的频数是4,频率是0.1知,
内的频数是4,频率是0.1知,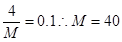 ,因为频数之和为40,所以4+24+m+2=40,m="10."
,因为频数之和为40,所以4+24+m+2=40,m="10." 
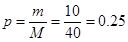 ---4分
---4分
因为a是对应分组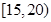 的频率与组距的商,所以
的频率与组距的商,所以 ----------6分
----------6分
(Ⅱ)因为该校高三学生有240人,分组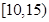 内的频率是0.25,
内的频率是0.25,
所以估计该校高三学生参加社区服务的次数在此区间内的人数为60人. ……----8分
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有m+2=6人,
设在区间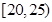 内的人为
内的人为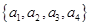 ,在区间
,在区间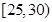 内的人为
内的人为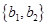 .
.
则任选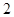 人共有
人共有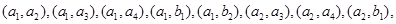
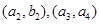 ,
,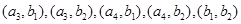 15种情况, ……10分
15种情况, ……10分
而两人都在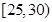 内只能是
内只能是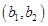 一种,所以所求概率为
一种,所以所求概率为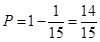
然后结合古典概型概率公式得到概率的求解。
(1)中由分组
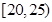 内的频数是4,频率是0.1,可知M的值和m的值
内的频数是4,频率是0.1,可知M的值和m的值(2)因为该校高三学生有240人,分组
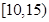 内的频率是0.25,从而得到人数为60人
内的频率是0.25,从而得到人数为60人((3)利用在区间
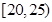 内的人为
内的人为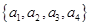 ,在区间
,在区间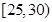 内的人为
内的人为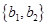 .
. 从中任意选两个人所有的基本事件数,得到事件A的基本事件数,运用概率公式得到。
解(Ⅰ)由分组
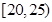 内的频数是4,频率是0.1知,
内的频数是4,频率是0.1知,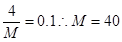 ,因为频数之和为40,所以4+24+m+2=40,m="10."
,因为频数之和为40,所以4+24+m+2=40,m="10." 
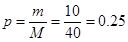 ---4分
---4分因为a是对应分组
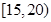 的频率与组距的商,所以
的频率与组距的商,所以 ----------6分
----------6分(Ⅱ)因为该校高三学生有240人,分组
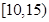 内的频率是0.25,
内的频率是0.25,所以估计该校高三学生参加社区服务的次数在此区间内的人数为60人. ……----8分
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有m+2=6人,
设在区间
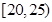 内的人为
内的人为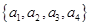 ,在区间
,在区间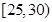 内的人为
内的人为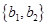 .
. 则任选
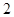 人共有
人共有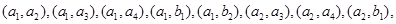
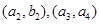 ,
,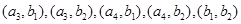 15种情况, ……10分
15种情况, ……10分而两人都在
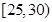 内只能是
内只能是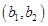 一种,所以所求概率为
一种,所以所求概率为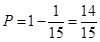

练习册系列答案
相关题目

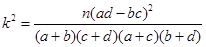
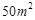 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)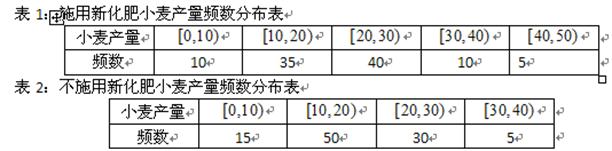
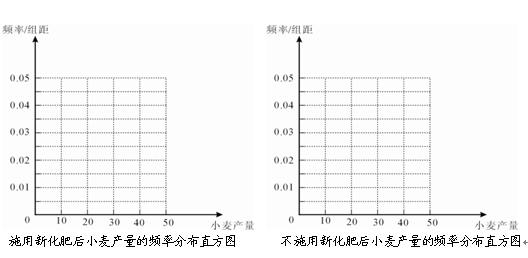
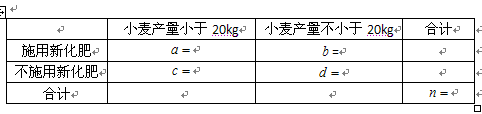
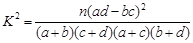
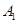 .
.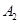 .….
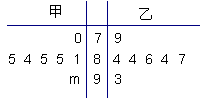
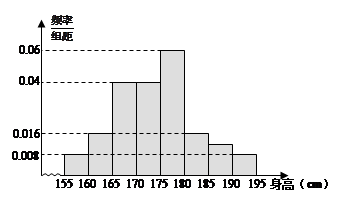
.….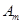 (如
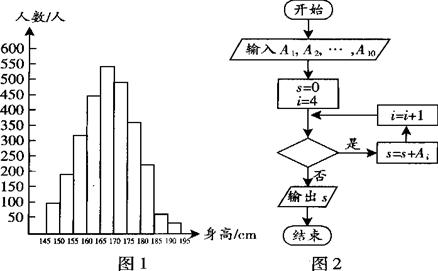
(如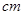 )在[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180
)在[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180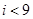 ?
?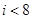 ?
?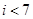 ?
? ?
?
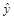 =1.5x-15,则下列结论正确的是( )
=1.5x-15,则下列结论正确的是( )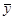 =1.5
=1.5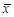 -15
-15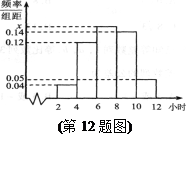
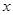 与销售额
与销售额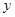 (单位:万元)之间有如下一组数据:
(单位:万元)之间有如下一组数据: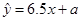 ,则
,则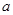 的值是( )
的值是( )