题目内容
1.已知f(x)是定义在R上的奇函数,当x>0 时,f(x)=1+($\frac{1}{2}$)x,则f(-2)=$-\frac{5}{4}$.分析 根据题意,先求出当x<0时,函数的解析式,然后代入数据计算即可.
解答 解:设x<0,则-x>0,
根据题意,有f(-x)=$1+(\frac{1}{2})^{-x}$=1+2x,
又f(x)是定义在R上的奇函数,
所以f(x)=-f(-x)=-(1+2x),
从而f(-2)=-(1+2-2)=$-\frac{5}{4}$,
故答案为:$-\frac{5}{4}$.
点评 本题考查利用单调性求函数的解析式,属于基础题.

练习册系列答案
相关题目
11.执行如图所示的程序框图,要使输出的S值小于1,则输入的t值不能是下面的( )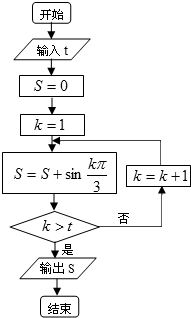

| A. | 2012 | B. | 2016 | C. | 2014 | D. | 2015 |
12.由曲线xy=1,直线y=x,x=3所围成封闭的平面图形的面积是( )
| A. | $\frac{32}{9}$ | B. | 4-ln3 | C. | 4+ln3 | D. | 2-ln3 |
6.设Sn是等差数列{an}的前n项和,已知a2=3,a6=11,则S7等于( )
| A. | 13 | B. | 49 | C. | 35 | D. | 63 |
 据统计某校学生在上学路上所需时间最多不超过120分钟.该校随机抽取部分新入校的新生其在上学路上所需时间(单位:分钟)进行调查,并将所得数据绘制成频率分布直方图.
据统计某校学生在上学路上所需时间最多不超过120分钟.该校随机抽取部分新入校的新生其在上学路上所需时间(单位:分钟)进行调查,并将所得数据绘制成频率分布直方图.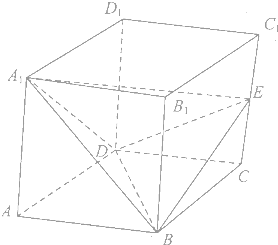 已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点
已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点