题目内容
在△ABC中,设内角A,B,C的对边分别为a,b,c向量| m |
| n |
| 2 |
| m |
| n |
(1)求角A的大小;
(2)若b=4
| 2 |
| 2 |
分析:(1)先根据向量模的运算表示出|
+
|2,然后化简成y=Asin(wx+ρ)+b的形式,再根据正弦函数的性质和|
+
|=2可求出A的值.
(2)先根据余弦定理求出a,c的值,再由三角形面积公式可得到最后答案.
| m |
| n |
| m |
| n |
(2)先根据余弦定理求出a,c的值,再由三角形面积公式可得到最后答案.
解答:解:(Ⅰ)∵
+
=(
+cosA-sinA,cosA+sinA)
∴|
+
|2=(
+cosA-sinA)2+(cosA+sinA)2
=2+2
(cosA-sinA)+(cosA-sinA)2+(cosA+sinA)2
=2+2
(cosA-sinA)+2=4-4sin(A-
)
∵|
+
|=2∴4-4sin(A-
)=4sin(A-
)=0
又∵0<A<π∴-
<A-
<
∴A-
=0,
∴A=
(Ⅱ)由余弦定理,a2=b2+c2-2bccosA,又b=4
,c=
a,A=
,得
a2=32+2a2-2×4
×
a•
,
即a2-8
+32=0,解得a=4
∴c=8
∴
=
b•csinA=
×4
×8×sin
=16
=
×(4
)2=16
| m |
| n |
| 2 |
∴|
| m |
| n |
| 2 |
=2+2
| 2 |
=2+2
| 2 |
| π |
| 4 |
∵|
| m |
| n |
| π |
| 4 |
| π |
| 4 |
又∵0<A<π∴-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
∴A=
| π |
| 4 |
(Ⅱ)由余弦定理,a2=b2+c2-2bccosA,又b=4
| 2 |
| 2 |
| π |
| 4 |
a2=32+2a2-2×4
| 2 |
| 2 |
| ||
| 2 |
即a2-8
| 2a |
| 2 |
∴
| S | △ABC |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| π |
| 4 |
| S | △ABC |
| 1 |
| 2 |
| 2 |
点评:本题主要考查向量的求模运算、余弦定理和三角形面积公式的应用.向量和三角函数的综合题是高考的热点问题,每年必考,要给予充分重视.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
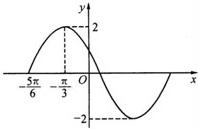 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的图象如图所示.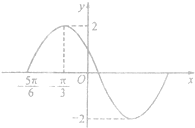 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的图象如图所示.