Question

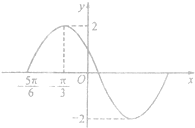已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜2π）在一个周期内的图象如图所示．
（1）求ω，φ的值；
（2）在△ABC中，设内角A、B、C所对边的长分别为a、b、c．若f（B）=-2，a=4，c=2，求b的值．

Answer 1

分析：（1）由题意可得 

1

4

×

2π

ω

=-

π

3

+

5π

6

，得ω=1，f（x）=2sin（x+∅），据f（-

π

3

 ）=2，及∅的范围
求出∅的值．
（2）在△ABC中，根据f（B）=-2=2sin（B+

5π

6

），及B的范围求出B值，由余弦定理可得  b 的值．

解答：解：（1）由题意可得 

1

4

×

2π

ω

=-

π

3

+

5π

6

，∴ω=1，故f（x）=2sin（x+∅）．
又f（-

π

3

 ）=2sin（-

π

3

+∅）=2，∴sin（-

π

3

+∅）=1，∴（-

π

3

+∅）=2kπ+

π

2

，k∈z，
∴∅=2kπ+

5π

6

，根据 0＜φ＜2π，∴∅=

5π

6

．
（2）在△ABC中，f（B）=-2=2sin（B+

5π

6

），∴sin（B+

5π

6

）=-1，根据 

5π

6

＜B+

5π

6

＜

11π

6

，
∴B+

5π

6

=

3π

2

，B=

2π

3

．由余弦定理可得 b²=a²+c²-2accosB 
=16+4-2×4×2（-

1

2

）=28，故 b=2

7

．

点评：本题考查根据函数的部分图象求函数的解析式，余弦定理的应用，根据三角函数的值求角，求出函数的解析式，是解题
的关键．