题目内容
在△ABC中，设内角A、B、C的对边分别为a、b、c，且tan(
-C)=
-2
（1）求角C的大小；
（2）若c=
且a+b=5求△ABC的面积．
| π |
| 4 |
| 3 |
（1）求角C的大小；
（2）若c=
| 7 |
分析：（1）利用两角和与差的正切函数，求出tanC的值，即可求出∠C；
（2）先利用c2=a2+b2-2abcosC，求出ab，然后根据△ABC的面积公式
absinC，求出面积．
（2）先利用c2=a2+b2-2abcosC，求出ab，然后根据△ABC的面积公式
| 1 |
| 2 |
解答：解：（1）∵tan(
-C)=
-2∴
=
-2（2分）
∴tanC=
（4分）
∵在△ABC中，0＜C＜π
∴C=
（6分）
（2）∵c2=a2+b2-2abcosC
∴7=a2+b2-ab=（a+b）2-3ab=25-3ab（8分）
∴ab=6∴S△ABC=
absinC=
．（12分）
| π |
| 4 |
| 3 |
| 1-tanC |
| 1+tanC |
| 3 |
∴tanC=
| 3 |
∵在△ABC中，0＜C＜π
∴C=
| π |
| 3 |
（2）∵c2=a2+b2-2abcosC
∴7=a2+b2-ab=（a+b）2-3ab=25-3ab（8分）
∴ab=6∴S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
点评：本题主要考查了两角和与差的正切函数和三角形的面积公式，注意巧用两角和与差的正切函数，求出tanC的值．
练习册系列答案
相关题目
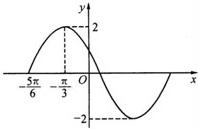已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜2π）在一个周期内的图象如图所示．
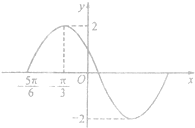已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜2π）在一个周期内的图象如图所示．