题目内容
港口
北偏东
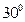方向的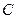
处有一检查站，港口正东方向的
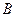处有一轮船，距离检查站为31海里，该轮船从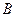处沿正西方向航行20海里后到达
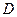处观测站，已知观测站与检查站距离21海里，问此时轮船离港口还有多远？
|
|
|
|
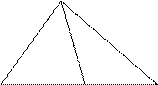
解析
练习册系列答案
相关题目
题目内容
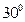港口北偏东方向的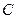处有一检查站，港口正东方向的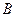处有一轮船，距离检查站为31海里，该轮船从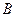处沿正西方向航行20海里后到达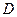处观测站，已知观测站与检查站距离21海里，问此时轮船离港口还有多远？
|
|
|
|
解析
中，若向量
且
与
共线
，求
的值.
的三个内角
所对的边分别为
，向量
，
，且
.
的大小；
；②
；③
，试从中再选择两个条件以确定
、
两点的距离为
海里，
处，甲船自
海里/小时的速度向
海里/小时的速度沿方位角
方向航行。问航行几小时两船之
间的距离最短？
，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往B处救援？（可能用到的数据
，
）
的南偏西
方向的
处，且与岛屿
的方向追赶渔船乙，刚好用2小时追上．
的值．
，
，若
相邻两对称轴间的距离为
。
的值
，并求
C的面积
，求边a的长。