Question

【题目】已知函数== ．

(1)求函数的单调递增区间;(只需写出结论即可)

(2)设函数= ,若在区间上有两个不同的零点,求实数的取值范围;

(3)若存在实数,使得对于任意的,都有成立,求实数的最大值．

Answer 1

【答案】（1）单调递增区间为（2）；（3）的最大值为.

【解析】试题分析：(1)画出函数图象,写出函数的单调区间即可;

(2)利用二次函数的判别式和端点函数值进行求解;

(3)利用函数的单调性求出两个函数的最值,通过比较两个最值进行求解．

试题解析：

函数的单调递增区间为

（2）

= = = ,

由题意知, 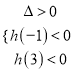即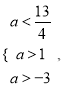

得.

（3）设函数= =

由题意, 在上的最小值不小于在上的最大值,

= = =

当或时, == =且在区间单调递增,

当时, = = ,

∴存在,使得成立,

即

,

的最大值为．