题目内容
 (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.(1)求截面BEFD与底面ABCD所成锐二面角的大小;
(2)求四棱锥A'-BEFD的体积.
分析:(1)连接AC、A'C',由正方体的结构特征可得:平面ACC'A'⊥BEFD,并且其交线为OO1,再过O1作垂直于底面的垂线交AC于O2,则∠O1OO2就是截面BEFD与底面ABCD所成角,再利用解三角形的有关知识求出答案即可.
(2)在△A′O1O中,A′O=
,A′01=O1O=
,所以由余弦定理可得:cos∠A′O1O进而求出sin∠A′O1O,所以点A'到平面BEFD的距离为:A′01•sin∠A′O1O=1,再结合题意求出SBEFD,进而求出几何体的体积.
(2)在△A′O1O中,A′O=
| ||
| 2 |
3
| ||
| 4 |
解答:解:(1)在棱长为1的正方体A'C中,连接AC、A'C',
因为BD⊥AA'、BD⊥AC,
所以平面ACC'A'⊥BEFD,并且其交线为OO1,
再过O1作垂直于底面的垂线交AC于O2,则∠O1OO2就是截面BEFD与底面ABCD所成角,
由题意可得,O1O2=1,OO2=
,
所以在Rt△O1O2O中有tan∠O1OO2=
=2
,
故截面BEFD与底面ABCD所成角为arctan2
;
(2)在△A′O1O中,由正方体的棱长为1可得:A′O=
,A′01=O1O=
,
所以由余弦定理可得:cos∠A′O1O=
,所以sin∠A′O1O=
,
所以点A'到平面BEFD的距离为:A′01•sin∠A′O1O=
×
=1,
所以点A'到平面BEFD的距离A′H是1,由上面O1O2=1,OO2=
,得OO1=
=
,
所以SBEFD=
•
=
,
所以四棱锥A'-BEFD的体积V=
SBEFD•A′H=
.
因为BD⊥AA'、BD⊥AC,
所以平面ACC'A'⊥BEFD,并且其交线为OO1,
再过O1作垂直于底面的垂线交AC于O2,则∠O1OO2就是截面BEFD与底面ABCD所成角,
由题意可得,O1O2=1,OO2=
| ||
| 4 |
所以在Rt△O1O2O中有tan∠O1OO2=
| 1 | ||||
|
| 2 |
故截面BEFD与底面ABCD所成角为arctan2
| 2 |
(2)在△A′O1O中,由正方体的棱长为1可得:A′O=
| ||
| 2 |
3
| ||
| 4 |
所以由余弦定理可得:cos∠A′O1O=
| 1 |
| 3 |
2
| ||
| 3 |
所以点A'到平面BEFD的距离为:A′01•sin∠A′O1O=
2
| ||
| 3 |
3
| ||
| 4 |
所以点A'到平面BEFD的距离A′H是1,由上面O1O2=1,OO2=
| ||
| 4 |
12+(
|
3
| ||
| 4 |
所以SBEFD=
| ||||||
| 2 |
3
| ||
| 4 |
| 9 |
| 8 |
所以四棱锥A'-BEFD的体积V=
| 1 |
| 3 |
| 3 |
| 8 |
点评:本题主要考查二面角与几何体的体积,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键;求几何体的体积的关键是求出点到底面的距离与底面的面积.

练习册系列答案
相关题目
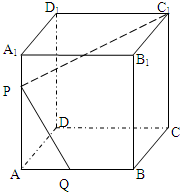 (理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.
(理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n. 如图,在棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是A1A,B1B的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是A1A,B1B的中点.