题目内容
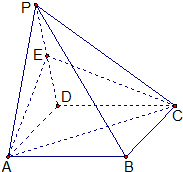 如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点.
如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点.(1)求证:PB∥平面EAC;
(2)若AD=2AB=2,求直线PB与平面ABCD所成角的正切值;
(3)当
| AD | AB |
分析:(1)要证PB∥平面EAC,根据线面平行的判定定理,只需证明PB平行于平面EAC中的一条直线.连接BD交AC于O,连接EO,因为O、E分别为BD、PD的中点,根据三角形的中位线的性质,可知EO∥PB,从而问题得证;
(2)设N为AD中点,连接PN,BN,则PN⊥AD,从而可得∠PBN为直线PB与平面ABCD所成的角,进而可求PB与平面ABCD所成角正切值;
(3)由(2)知,NB为PB在面ABCD上的射影,要使PB⊥AC,需且只需NB⊥AC,利用Rt△NAB∽Rt△CBA,可求得
=
时,PB⊥AC.
(2)设N为AD中点,连接PN,BN,则PN⊥AD,从而可得∠PBN为直线PB与平面ABCD所成的角,进而可求PB与平面ABCD所成角正切值;
(3)由(2)知,NB为PB在面ABCD上的射影,要使PB⊥AC,需且只需NB⊥AC,利用Rt△NAB∽Rt△CBA,可求得
| AD |
| AB |
| 2 |
解答: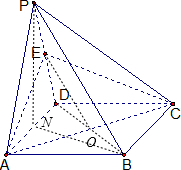 (1)证明:连接BD交AC于O,连接EO,
(1)证明:连接BD交AC于O,连接EO,
因为O、E分别为BD、PD的中点,
所以EO∥PB,…(2分)
因为E0?平面EAC,PB?平面EAC,
所以PB∥平面EAC.…(4分)
(2)解:设N为AD中点,连接PN,BN,则PN⊥AD…(5分)
又面PAD⊥底面ABCD,
所以PN⊥底面ABCD…(6分)
所以∠PBN为直线PB与平面ABCD所成的角,…(7分)
又AD=2AB=2,则PN=
,NB=
,…(8分)
所以tan∠PBN=
=
,
即PB与平面ABCD所成角正切为值
…(9分)
(3)由(2)知,NB为PB在面ABCD上的射影,要使PB⊥AC,需且只需NB⊥AC.(10分)
在矩形ABCD中,设AD=1,AB=x,AN=
,
由∠ANB=∠BAC,得Rt△NAB∽Rt△CBA,…(11分)
=
⇒AB2=AN•BC⇒x2=
解之得:x=
,…(13分)
所以,当
=
时,PB⊥AC.…(14分)
 (1)证明:连接BD交AC于O,连接EO,
(1)证明:连接BD交AC于O,连接EO,因为O、E分别为BD、PD的中点,
所以EO∥PB,…(2分)
因为E0?平面EAC,PB?平面EAC,
所以PB∥平面EAC.…(4分)
(2)解:设N为AD中点,连接PN,BN,则PN⊥AD…(5分)
又面PAD⊥底面ABCD,
所以PN⊥底面ABCD…(6分)
所以∠PBN为直线PB与平面ABCD所成的角,…(7分)
又AD=2AB=2,则PN=
| 3 |
| 2 |
所以tan∠PBN=
| ||
|
| ||
| 2 |
即PB与平面ABCD所成角正切为值
| ||
| 2 |
(3)由(2)知,NB为PB在面ABCD上的射影,要使PB⊥AC,需且只需NB⊥AC.(10分)
在矩形ABCD中,设AD=1,AB=x,AN=
| 1 |
| 2 |
由∠ANB=∠BAC,得Rt△NAB∽Rt△CBA,…(11分)
| AN |
| AB |
| AB |
| BC |
| 1 |
| 2 |
解之得:x=
| ||
| 2 |
所以,当
| AD |
| AB |
| 2 |
点评:本题考查的重点是线面垂直的判定,面面垂直的性质,线面角,解题的关键是正确运用线面垂直的判定,正确作出线面角,有综合性.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=