题目内容
(本题满分12)
定义在R上的函数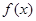 满足
满足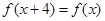 ,当2≤x≤6时,
,当2≤x≤6时,
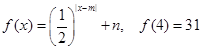 。
。
(1)求m ,n的值;
(2)比较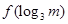 与
与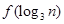 的大小
的大小
【答案】
(1)m =4,n=30
(2)f(log3 m)<f(log3 n)
【解析】解: (1)∵f(x)在R上满足f (x+4)=f (x),∴4是f(x)的一个周期.∴f (2)= f (6)…(2分)
∴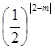 +n=
+n=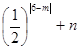 ①,
①,
又∵f (4)=31,∴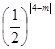 +n=31 ② ……………(4分)
+n=31 ② ……………(4分)
联解①、②组成的方程组,得m =4,n=30…………………(6分).
(2)由(1)知,f(x)=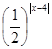 +30,x∈
+30,x∈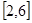 .
.
∵1<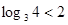 , ∴5<
, ∴5<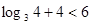 .∴f(log3 m)= f(log3 4)=f(
.∴f(log3 m)= f(log3 4)=f(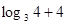 )
)
=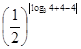 =
=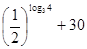 ……………………………(8分)
……………………………(8分)
又∵3<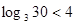 ,∴f(log3 n)= f(log3 30)=
,∴f(log3 n)= f(log3 30)=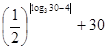
=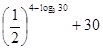 =
=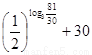 …………………(10分)
…………………(10分)
∵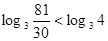 ,∴
,∴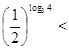
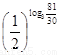
∴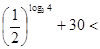
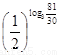 +30,∴f(log3 m)<f(log3 n)………(12分).
+30,∴f(log3 m)<f(log3 n)………(12分).

练习册系列答案
相关题目
 中,设点
中,设点 ,直线
,直线 :
: ,点
,点 在直线
在直线 是线段
是线段 与
与 轴的交点,
轴的交点,  .
.
 的轨迹的方程
的轨迹的方程 ;
; 过
过 ,且圆心
,且圆心 是圆
是圆 是否为定值?请说明理由.
是否为定值?请说明理由. (
( )的一个顶点与抛物线 C2:
)的一个顶点与抛物线 C2: 的焦点重合,F1,F2 分别是椭圆的左、右焦点,离心率
的焦点重合,F1,F2 分别是椭圆的左、右焦点,离心率  ,过椭圆右焦点 F2 的直线
,过椭圆右焦点 F2 的直线  与椭圆 C 交于 M,N 两点.
与椭圆 C 交于 M,N 两点. ,若存在,求出直线
,若存在,求出直线
 为定值.
为定值. 个时,零件的实际出厂单价为P元,写出函数的表达式;
个时,零件的实际出厂单价为P元,写出函数的表达式; 是定义在
是定义在 上的增函数,令
上的增函数,令
 时定值;
时定值; 在
在 ,求证
,求证 。
。 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。 的方程;
的方程; 的面积S的最大值;
的面积S的最大值;