题目内容
(本题满分12分)
如图,斜率为1的直线 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。
(1)若|AB|=8,求抛物线 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)

【答案】
(1)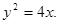
(2)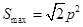
(3)证明见解析。
【解析】
解:设
(1)由条件知直线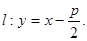
由 消去y,得
消去y,得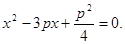 …………1分
…………1分
由题意,判别式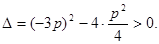 (不写,不扣分)
(不写,不扣分)
由韦达定理,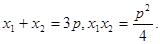
由抛物线的定义,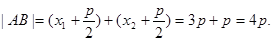
从而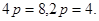 所求抛物的方程为
所求抛物的方程为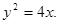 …………3分
…………3分
(2)设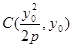 。由(1)易求得
。由(1)易求得
则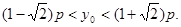 …………4分
…………4分
点C到直线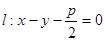 的距离
的距离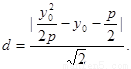
将原点O(0,0)的坐标代入直线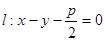 的左边,
的左边,
得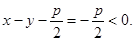
而点C与原点O们于直线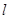 的同侧,由线性规划的知识知
的同侧,由线性规划的知识知
因此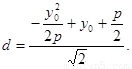 …………6分
…………6分
由(1),|AB|=4p。
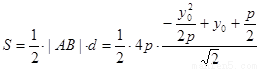
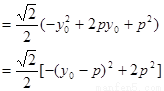
由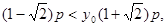
知当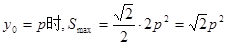 …………8分
…………8分
(3)由(2),易得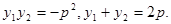
设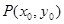 。
。
将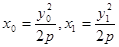 代入直线PA的方程
代入直线PA的方程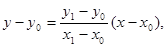
得
同理直线PB的方程为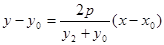
将 代入直线PA,PB的方程得
代入直线PA,PB的方程得
 …………10分
…………10分

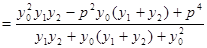

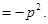 …………12分
…………12分

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面