题目内容
【题目】已知函数f（x）=x|2x﹣a|﹣1．
①当a=0时，不等式f（x）+1＞0的解集为_____；
②若函数f（x）有三个不同的零点，则实数a的取值范围是_____．
【答案】（0，+∞） （2
，+∞）
【解析】
①把a=0代入函数解析式，可得不等式，对x分类求解得答案；
②转化方程的根为两个函数的图象的交点，利用数形结合，通过函数的导数求解即可．
①当a=0时，不等式f（x）+1＞0x|2x|﹣1+1＞0，
即2x|x|＞0，
若x＜0，得﹣2x2＞0，不合题意；
若x=0，得0＞0，不合题意；
若x＞0，得2x2＞0，则x＞0．
综上，当a=0时，不等式f（x）+1＞0的解集为（0，+∞）；
②若函数f（x）有三个不同的零点，即方程x|2x﹣a|﹣1=0有3个不同根．
即|2x﹣a|
有三个解，
令y=|2x﹣a|，则y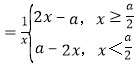
，画出两个函数的图象，如图：
x
，y，由y′
2，解得x
，x
（舍去），
此时切点坐标（
），代入y=a﹣2x，可得a=2
2，
函数f（x）=x|2x﹣a|﹣1有三个零点，
则实数a的取值范围为（2，+∞）．
故答案为：（0，+∞）；（2，+∞）．
练习册系列答案
相关题目
